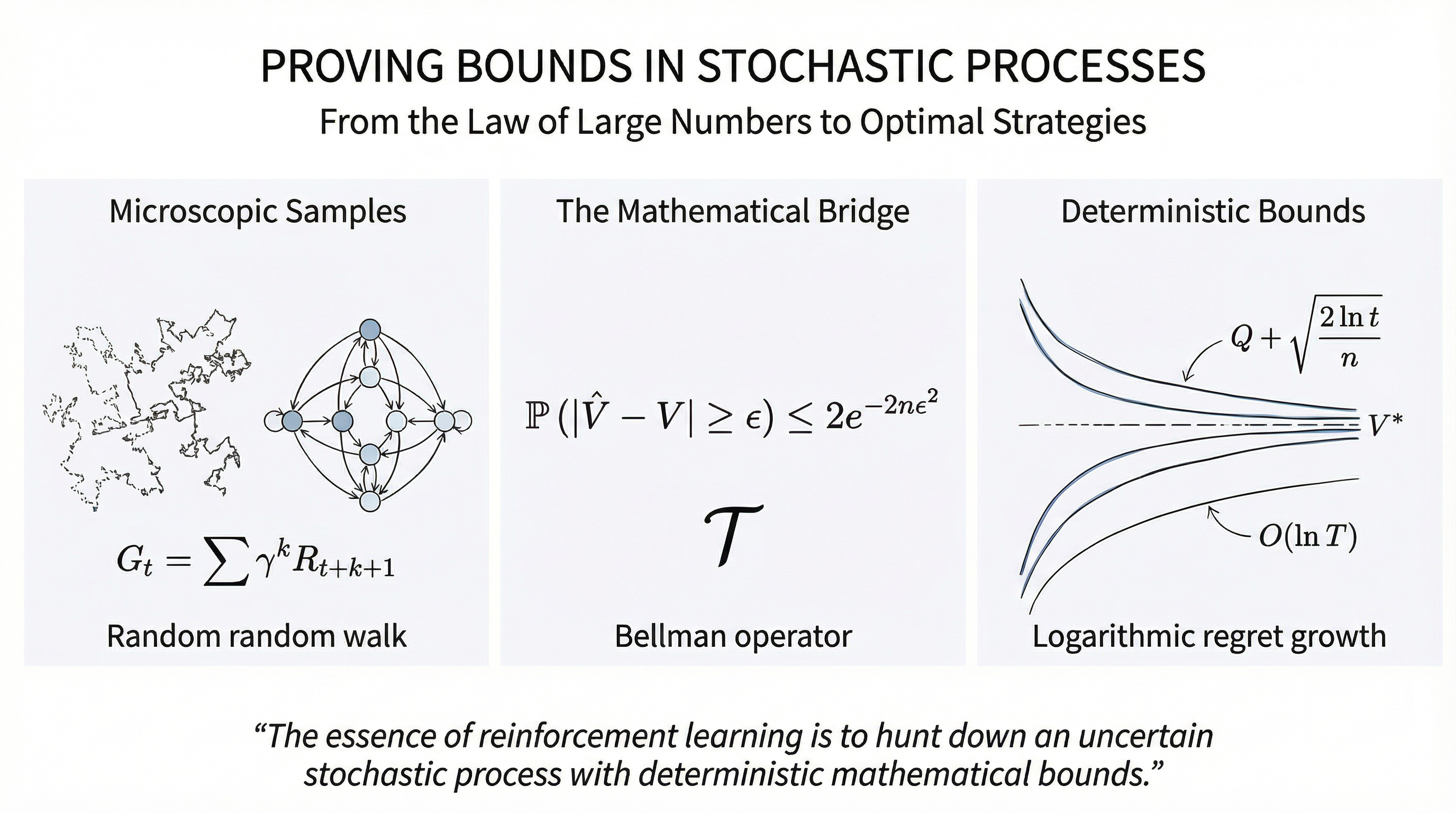
The essence of reinforcement learning is to hunt down an uncertain stochastic process with deterministic mathematical bounds. All our efforts are to make these bounds ever tighter.

"Chance is only the measure of our ignorance." — Henri Poincaré

---

为了在随机环境中构建最优决策序列，我们首先必须剥离感性的“经验”，转而寻求一种类似于力学公理的数学表述。在经典的物理范式中，系统的演化由初始条件与确定性的微分方程共同决定；而在智能体（Agent）互动的范式下，我们面对的是一种更加混沌的动力学：系统不仅受制于环境的随机波动，还受制于智能体干预产生的路径偏差。本笔记将摒弃一切算法实现的枝节，从第一性原理出发，推演序列决策如何从随机过程演化为确定的算子收敛问题。

The mechanical foundation of sequential decision-making: MDP (Markov Decision Process)

建立决策理论的首要任务是精确定义状态空间及其演化律。我们定义一个由状态空间 $\mathcal{S}$ 和动作空间 $\mathcal{A}$ 张成的交互空间。在任意时间索引 $t$，系统的瞬时构型由 $S_t \in \mathcal{S}$ 描述，而智能体施加的外部干预为 $A_t \in \mathcal{A}$。系统的演化遵循转移核 $P(s' \mid s, a)$，这在本质上是状态空间 $\mathcal{S}$ 上概率测度的映射，定义了特定扰动下的统计演化律。

马尔可夫决策过程（MDP）的结构完整性建立在马尔可夫公设之上。该性质断言，系统未来的演化仅取决于当前状态 $S_t$，而与历史轨迹 $\{S_0, \dots, S_{t-1}\}$ 条件独立。在测度论的语言中，条件分布满足：

$$\begin{equation} \mathbb{P}(S_{t+1} \mid S_t, A_t, \dots, S_0, A_0) = \mathbb{P}(S_{t+1} \mid S_t, A_t) \end{equation}$$

这意味着 $S_t$ 代表了历史信息的完全坍缩，作为预测未来结果的充分统计量。若无此性质，决策将退化为高维路径上的泛函优化；而在马尔可夫假设下，动态演化被转化为 $\mathcal{S}$ 上的局部代数递归。为了衡量演化的效用，我们引入标量奖励 $R(s, a)$，代表从环境中提取的瞬时“功”或“负熵”。我们的目标并非即时奖励的最大化，而是累积回报的期望，即价值函数 $V^\pi(s)$。为确保无穷级数的收敛，引入折扣因子 $\gamma \in [0, 1)$，它在数学上充当收缩系数，在物理上量化了系统的时间视界。

贝尔曼算子与不动点定理一旦确立了 MDP 框架，决策目标便转化为寻找一个最优策略 $\pi^* \in \mathcal{A}^{\mathcal{S}}$，以最大化从任意状态出发的期望回报。通过全期望公式，我们发现价值函数 $V^\pi$ 具有一种递归结构，即贝尔曼期望方程：

$$\begin{equation} V^\pi(s) = \sum_{a \in \mathcal{A}} \pi(a|s) \left[ R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s' \mid s, a) V^\pi(s') \right] \end{equation}$$

该方程的深刻之处在于它将全局无穷轨迹的求和转化为局部的算子映射。我们可以定义一个线性贝尔曼算子 $\mathcal{T}^\pi: \mathbb{R}^{|\mathcal{S}|} \to \mathbb{R}^{|\mathcal{S}|}$。在泛函分析的语境下，价值函数 $V^\pi$ 恰恰是该算子的不动点。

Complete Metric Spaces and Bellman Operators

我们定义一个函数空间 $\mathcal{V}$，其中包含所有定义在状态空间 $\mathcal{S}$ 上的有界实值函数 $V: \mathcal{S} \to \mathbb{R}$。为了量化两个价值估计之间的“距离”，我们引入无穷范数（$L_\infty$ norm）作为度量准则：

$$\begin{equation} d(V, U) = \|V - U\|_\infty = \max_{s \in \mathcal{S}} |V(s) - U(s)| \end{equation}$$

在此度量下，$(\mathcal{V}, \|\cdot\|_\infty)$ 构成一个巴拿赫空间（Banach Space），即一个完备的赋范向量空间。这意味着，在该空间内任何满足柯西判别准则的函数序列，其极限必然存在且仍在该空间内。这一完备性是证明收敛性的先决条件。在此空间上，我们定义最优贝尔曼算子 $\mathcal{T}^*: \mathcal{V} \to \mathcal{V}$，其作用是将一个价值估计映射为经过一步推演后的新估计：

$$\begin{equation} (\mathcal{T}^* V)(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s' \mid s, a) V(s') \right] \end{equation}$$

压缩映射性质的数理推导为了证明 $\mathcal{T}^*$ 的收敛性，我们必须验证其满足压缩映射（Contraction Mapping）的定义。即证明对于任意 $V, U \in \mathcal{V}$，应用算子后的距离将严格小于应用前的距离：

$$\begin{equation} \|\mathcal{T}^* V - \mathcal{T}^* U\|_\infty \le \gamma \|V - U\|_\infty, \quad \gamma < 1 \end{equation}$$

证明过程：考虑任意状态 $s \in \mathcal{S}$。不失一般性，假设 $(\mathcal{T}^* V)(s) \ge (\mathcal{T}^* U)(s)$。令 $a^*$ 为使 $V$ 在状态 $s$ 下达到最优值的动作，即 $a^* = \arg\max_a [R_{s,a} + \gamma \mathbb{E}[V'] ]$。根据 $\max$ 算子的性质，我们有：

$$\begin{equation} \begin{aligned} (\mathcal{T}^* V)(s) - (\mathcal{T}^* U)(s) &= \max_a [R_{s,a} + \gamma \mathbb{E}[V'] ] - \max_a [R_{s,a} + \gamma \mathbb{E}[U'] ] \\ &\le [R_{s,a^*} + \gamma \mathbb{E}[V'] ] - [R_{s,a^*} + \gamma \mathbb{E}[U'] ] \\ &= \gamma \sum_{s' \in \mathcal{S}} P(s' \mid s, a^*) (V(s') - U(s')) \\ &\le \gamma \sum_{s' \in \mathcal{S}} P(s' \mid s, a^*) |V(s') - U(s')| \\ &\le \gamma \sum_{s' \in \mathcal{S}} P(s' \mid s, a^*) \|V - U\|_\infty \\ &= \gamma \|V - U\|_\infty \end{aligned} \end{equation}$$

由于该不等式对所有状态 $s$ 均成立，我们可以得出结论：$\|\mathcal{T}^* V - \mathcal{T}^* U\|_\infty \le \gamma \|V - U\|_\infty$。现在我们从数理上严谨地证明了贝尔曼算子在无穷范数下是一个系数为 $\gamma$ 的压缩映射。巴拿赫不动点定理的推导标志着本笔记“确定性”部分的终结。它告诉我们，如果能精确执行算子 $\mathcal{T}^*$，真理的获取仅仅是一个迭代时间的问题。

所以根据巴拿赫不动点定理（Banach Fixed-Point Theorem），由于 $\gamma < 1$，算子 $\mathcal{T}^\pi$ 在 $L_\infty$ 范数下是一个收缩映射。这确保了从任何初始估计 $V_0$ 出发，重复应用算子都将指数级地收敛至唯一的真实价值函数。这种确定性的收敛为决策论提供了代数上的可行性保证。即使扩展到非线性的贝尔曼最优方程 $\mathcal{T}^* V(s) = \max_a [R(s, a) + \gamma \mathbb{E}[V(s') \mid s, a]]$，由于算子的单调性与收缩性，最优价值 $V^*$ 的存在性与唯一性依然稳固。所以我们的目标从复杂的序列搜索简化成了在价值空间中寻找算子不动点的过程。

估计的裂痕与缩放的必然性尽管贝尔曼方程在解析上趋于完美，但在强化学习的实战范式中，我们遭遇了根本性的障碍：转移核 $P$ 和奖励分布 $R$ 对智能体而言通常是黑盒。我们无法进行精确的算子积分，而必须依赖通过交互产生的经验轨迹 $\tau = \{s_0, a_0, r_1, s_1, \dots\}$。这一转变标志着我们从线性代数的确定性世界跨入了统计推断的波动世界。价值估计 $\hat{V}(s)$ 变成了随机变量 $G_t$ 的经验均值。虽然大数定律（LLN）保证了当样本量 $n \to \infty$ 时，$\hat{V}(s)$ 最终会收敛于真实期望，但在有限时间尺度内，这种收敛极不稳定。

因此，关于“无知边界”的关键问题浮出水面：在给定有限样本的情况下，我们的估计值 $\hat{V}(s)$ 偏离真实不动点 $V^*$ 多远？若估计误差显著，由此推导的任何策略改进都可能导致系统性偏差。纯粹的力学路径在此达到了极限。理论的进一步演进必须寻求集中不等式（Concentration Inequalities）的庇护。我们不再仅仅询问“是否”收敛，而是询问“以何种速率”以及“以多大概率”保持在特定界限内。对误差概率上界的追求，构成了从马尔可夫不等式、切比雪夫不等式演进到霍夫丁引理的逻辑动因。这套数学工具库对于将原始随机波动转化为可控的置信区间至关重要，为智能体在未知世界中的探索（Exploration）提供了严谨的数理基石。

From rectangular scaling to Chebyshev

我们无法直接观测到算子中的期望 $\mathbb{E}$，而只能观测到经验均值 $\hat{\mu}_n$。这种从“无限次实验”到“必须在有限次采样”的 gap 中，我们需要引入了统计学中的不确定性。为了量化这种不确定性，我们需引入浓度不等式（Concentration Inequalities）。这类不等式的作用是给出尾部概率（Tail Probability）的上界，即：当样本量为 $n$ 时，估计值偏离真实值超过 $\epsilon$ 的概率有多大？

我们将从最粗糙的一阶矩放缩开始进行分析推导。

马尔可夫不等式试图回答的问题是：一阶矩的粗糙边界如果我们对随机变量的分布一无所知，仅知道它的均值（一阶矩），我们能对它的波动做出什么承诺？

对于一个非负随机变量 $X \ge 0$，给定任何常数 $a > 0$，其分布的尾部被其期望值 $\mathbb{E}[X]$ 所约束：

$$\begin{equation} \mathbb{P}(X \ge a) \le \frac{\mathbb{E}[X]}{a} \end{equation}$$

证明过程：引入指示函数 $\mathbb{I}_{X \ge a}$。由于当 $X \ge a$ 时，$\frac{X}{a} \ge 1 \ge \mathbb{I}_{X \ge a}$；当 $X < a$ 时，$\frac{X}{a} \ge 0 = \mathbb{I}_{X \ge a}$。因此，对于所有 $X \ge 0$，总有 $\mathbb{I}_{X \ge a} \le \frac{X}{a}$。对等式两边同时取期望：

$$\begin{equation} \mathbb{E}[\mathbb{I}_{X \ge a}] \le \mathbb{E}\left[\frac{X}{a}\right] \implies \mathbb{P}(X \ge a) \le \frac{\mathbb{E}[X]}{a} \end{equation}$$

马尔可夫不等式是极为“慷慨”且粗糙的。它仅仅利用了均值信息，对偏离的约束力呈线性衰减。在强化学习中，这意味着如果我们只知道平均奖励，我们对“偶尔出现极端坏结果”的防御力几乎为零。然而，它作为所有高级不等式的祖先，奠定了利用矩信息换取概率边界的底层逻辑。

随后切比雪夫不等式为了获得更紧（Tighter）的边界引用二阶矩和方差来介入，所以我们必须引入更高阶的信息。这里我们规定如果我们不仅知道均值 $\mu$，还知道变量波动的剧烈程度——方差 $\sigma^2$（二阶矩），我们就能利用切比雪夫不等式（Chebyshev's Inequality）来实现平方级的收缩。

对于任意随机变量 $X$（不要求非负），若其期望为 $\mu$，方差为 $\sigma^2$，则对于任意 $\epsilon > 0$：

$$\begin{equation} \mathbb{P}(|X - \mu| \ge \epsilon) \le \frac{\sigma^2}{\epsilon^2} \end{equation}$$

证明过程：观察事件 $\{|X - \mu| \ge \epsilon\}$，这等价于变量 $(X - \mu)^2 \ge \epsilon^2$。由于 $(X - \mu)^2$ 是一个非负随机变量，我们对其应用马尔可夫不等式：

$$\begin{equation} \mathbb{P}((X - \mu)^2 \ge \epsilon^2) \le \frac{\mathbb{E}[(X - \mu)^2]}{\epsilon^2} \end{equation}$$

根据方差的定义 $\mathbb{E}[(X - \mu)^2] = \sigma^2$，得证：

$$\begin{equation} \mathbb{P}(|X - \mu| \ge \epsilon) \le \frac{\sigma^2}{\epsilon^2} \end{equation}$$

相比马尔可夫不等式的线性衰减，切比雪夫不等式表现出了平方级收敛。这意味着，只要方差有限，随着偏离阈值 $\epsilon$ 的增加，发生极值风险的概率将以 $1/\epsilon^2$ 的速度坠落。在智能体的价值估计中，如果我们能估算出回报的方差，就能初步给出一个置信区间，将原本混沌的随机游走框定在一定的方差范围之内。

$1/\epsilon^2$ 的衰减在面对大规模采样时仍然太慢。在机器学习中，我们通常追求的是指数级收敛。当我们考虑 $n$ 个独立样本的均值 $\bar{X}_n$ 时，切比雪夫给出的边界是 $\frac{\sigma^2}{n\epsilon^2}$。虽然它随着 $n$ 的增加而收缩，但其收缩效率远低于真实的物理分布。

这促使我们思考一个终极命题：如果我们不仅利用一阶矩和二阶矩，而是利用所有阶矩的信息（即通过矩生成函数 $M_X(t) = \mathbb{E}[e^{tX}]$ 进行放缩），会发生什么？这种将随机变量映射到指数空间的操作，将把马尔可夫不等式的线性放缩转化为对数空间的指数放缩。

Hoeffding's inequality

在处理诸如“智能体需要多少样本才能以 99% 的信心判定一个动作是次优的”这类问题时，平方级收敛的速度依然太慢。在强化学习中，由于我们通常处理的是有界奖励（如 $r \in [0, 1]$），我们实际上拥有比“方差有限”更强的数理性质——有界性（Boundedness）。

我们假设 $X_1, X_2, \dots, X_n$ 是独立随机变量，且 $X_i \in [a_i, b_i]$，均值为 $\mu_i$。我们要计算 $\mathbb{P}(\sum X_i - \sum \mu_i \ge t)$ 的上界。

直接计算概率分布通常很难，所以我们利用指数函数的单调性和马尔可夫不等式。

$$\mathbb{P}(Z \ge a) \le \frac{\mathbb{E}[Z]}{a}$$

但是我们知道马尔可夫不等式要求随机变量必须是非负的，但是 $(X_i - \mu_i)$ 代表的是偏差，它显然有正有负。所以，直接对原始误差项使用马尔可夫不等式在数学上是不合规的。直接套用，结果就变成了：

$$\mathbb{E}[\sum (X_i - \mu_i)] = \sum (\mathbb{E}[X_i] - \mu_i) = \sum (\mu_i - \mu_i) = 0$$ $$\mathbb{P}(\dots \ge t) \le \frac{0}{t} = 0$$

得到的结果是没有任何关于概率分布的有效信息。所以我们引入了一个单调递增的指数函数，做到了强制非负，且指数函数能把较大的偏差极度放大：

$$\begin{equation} \mathbb{P}\left(\sum (X_i - \mu_i) \ge t\right) = \mathbb{P}\left(e^{s \sum (X_i - \mu_i)} \ge e^{st}\right) \end{equation}$$

随后根据马尔克夫不等式，我们得到：

$$\begin{equation} \mathbb{P}\left(\sum (X_i - \mu_i) \ge t\right) \le e^{-st} \mathbb{E}\left[e^{s \sum (X_i - \mu_i)}\right] \end{equation}$$

利用变量的独立性，累加的期望变成了期望的乘积：

$$\begin{equation} \mathbb{P}(\dots) \le e^{-st} \prod_{i=1}^n \mathbb{E}\left[e^{s(X_i - \mu_i)}\right] \end{equation}$$

至此我们得到切尔诺夫界（Chernoff Bound）的通用形式：

$$\begin{equation} \mathbb{P}(X \ge \epsilon) = \mathbb{P}(e^{sX} \ge e^{s\epsilon}) \le \frac{\mathbb{E}[e^{sX}]}{e^{s\epsilon}} = e^{-s\epsilon} M_X(s) \end{equation}$$

其中 $M_X(s) = \mathbb{E}[e^{sX}]$ 被称为矩生成函数（MGF）。

这个技巧的精妙之处在于它引入了一个自由参数 $s$。我们可以通过优化 $s$ 来找到一个最紧的边界。它不再只是利用均值或方差，而是利用了 $X$ 的所有高阶矩信息，将其映射到了一个指数空间。霍夫丁引理是把有界变量的高斯包络为了继续推导，我们需要为 $M_X(s)$ 找到一个上界。对于一般的分布，这很难；但对于有界随机变量，霍夫丁引理提供了一个极其优美的缩放。

引理： 设 $X$ 是一个均值为 0 的随机变量，且 $X \in [a, b]$。对于任何 $s \in \mathbb{R}$：

$$\begin{equation} \mathbb{E}[e^{sX}] \le e^{\frac{s^2(b-a)^2}{8}} \end{equation}$$

证明思路：利用指数函数的凸性。对于任何 $x \in [a, b]$，它可以表示为 $a$ 和 $b$ 的凸组合：

$$\begin{equation} x = \frac{b-x}{b-a}a + \frac{x-a}{b-a}b \end{equation}$$

根据 Jensen 不等式（或直接利用 $e^{sx}$ 的凸性）：

$$\begin{equation} e^{sx} \le \frac{b-x}{b-a}e^{sa} + \frac{x-a}{b-a}e^{sb} \end{equation}$$

对两边取期望 $\mathbb{E}$，并注意到 $\mathbb{E}[X]=0$：

$$\begin{equation} \mathbb{E}[e^{sX}] \le \frac{b}{b-a}e^{sa} - \frac{a}{b-a}e^{sb} \end{equation}$$

为了简化证明，我们引入两个辅助变量：

令 $p = \frac{-a}{b-a}$。注意到由于 $\mathbb{E}[X]=0$，必有 $a \le 0 \le b$，因此 $p \in [0, 1]$。且 $1-p = \frac{b}{b-a}$。

令 $u = s(b-a)$。

此时，上述不等式的右侧可以重新表述为关于 $u$ 的函数 $\phi(u)$：

$$\begin{equation} \phi(u) = (1-p)e^{-pu} + pe^{(1-p)u} \end{equation}$$

我们的目标是证明 $\phi(u) \le e^{u^2/8}$。

定义函数 $L(u) = \ln \phi(u)$。如果能证明 $L(u) \le \frac{u^2}{8}$，则原命题成立。

$$\begin{equation} L(u) = \ln \left( (1-p)e^{-pu} + pe^{(1-p)u} \right) \end{equation}$$

将其展开：

$$\begin{equation} L(u) = -pu + \ln \left( 1 - p + pe^u \right) \end{equation}$$

我们对 $L(u)$ 在 $u=0$ 处进行泰勒展开。首先计算其各阶导数：

一阶导数：

$$\begin{equation} L'(u) = -p + \frac{pe^u}{1 - p + pe^u} \end{equation}$$

代入 $u=0$ 得：$L'(0) = -p + \frac{p}{1} = 0$。

二阶导数：令 $q(u) = \frac{pe^u}{1 - p + pe^u}$，则 $L'(u) = -p + q(u)$。

$$\begin{equation} L''(u) = q'(u) = \frac{p e^u (1-p+pe^u) - (pe^u)^2}{(1-p+pe^u)^2} = \frac{pe^u(1-p)}{(1-p+pe^u)^2} \end{equation}$$

观察可知，$L''(u)$ 的形式实际上是 $q(u)(1-q(u))$。

根据泰勒公式（带拉格朗日余项），存在一个 $\xi$ 介于 $0$ 与 $u$ 之间，使得：

$$\begin{equation} L(u) = L(0) + L'(0)u + \frac{1}{2} L''(\xi)u^2 \end{equation}$$

我们已知：$L(0) = \ln(1-p+p) = 0$。$L'(0) = 0$。对于任意实数 $z$，函数 $f(z) = z(1-z)$ 的极大值为 $\frac{1}{4}$（当 $z = 1/2$ 时取得）。由于 $q(\xi) = \frac{pe^\xi}{1-p+pe^\xi}$ 的值域在 $(0, 1)$ 内，因此：

$$\begin{equation} L''(\xi) = q(\xi)(1-q(\xi)) \le \frac{1}{4} \end{equation}$$

将这些结果代入泰勒展开式：

$$\begin{equation} L(u) \le 0 + 0 + \frac{1}{2} \cdot \frac{1}{4} \cdot u^2 = \frac{u^2}{8} \end{equation}$$

最后，我们将 $u = s(b-a)$ 代回：

$$\begin{equation} \ln(\mathbb{E}[e^{sX}]) \le L(s(b-a)) \le \frac{s^2(b-a)^2}{8} \end{equation}$$

两边同时取指数，即得霍夫丁引理的最终形式：

$$\begin{equation} \mathbb{E}[e^{sX}] \le \exp\left( \frac{s^2(b-a)^2}{8} \right) \end{equation}$$

这个推导揭示了霍夫丁不等式：在任何有界随机变量的波动，对数矩生成空间中，都被一个方差为 $\frac{(b-a)^2}{4}$ 的正态分布所“包络”。公式中的 $1/8$ 来自于两个 $1/2$ 的乘积：一个是泰勒展开的二阶项系数 $1/2$，另一个是二次函数 $z(1-z)$ 的最大值 $1/4$。

霍夫丁不等式：概率浓缩的终极形态将霍夫丁引理代入切尔诺夫界，并考虑 $n$ 个独立同分布的随机变量 $X_1, \dots, X_n$，其均值为 $\mu$，范围为 $[a, b]$。设 $\bar{X}_n = \frac{1}{n} \sum X_i$ 为经验平均。经过对参数 $s$ 的求导优化（令 $s = \frac{4n\epsilon}{(b-a)^2}$），我们得到著名的霍夫丁不等式（Hoeffding's Inequality）：

$$\begin{equation} \mathbb{P}(\bar{X}_n - \mu \ge \epsilon) \le \exp\left( - \frac{2n\epsilon^2}{(b-a)^2} \right) \end{equation}$$

从无知到信心的飞跃霍夫丁不等式的出现，很好的改变了智能体对不确定性的理解。我们可以从这个公式中得出几个结论：样本量 $n$ 的威力：误差概率随 $n$ 呈指数级下降。这意味着，如果你想让错误率降低 10 倍，你不需要 10 倍的样本，而只需要线性增加一小段样本。置信区间（Bound）的倒推：如果我们将错误率设为 $\delta$，即令 $\exp(-2n\epsilon^2) = \delta$，我们可以反解出误差 $\epsilon$：

$$\begin{equation} \epsilon = \sqrt{\frac{\ln(1/\delta)}{2n}} \end{equation}$$

这就是为什么在 UCB（置信上限）算法中，探索项总是包含 $\sqrt{\ln(t)/n}$。霍夫丁不等式证明了，只要我们采样足够多，我们就能以“大概率（1-$\delta$）”保证估计是“近似正确（误差 $<\epsilon$）”的。

Mathematical derivation of the UCB algorithm

在建立了霍夫丁不等式的指数级缩放之后，我们终于拥有了量化的工具。在强化学习的语境下，这种无知体现为智能体面临的探索与利用（Exploration vs. Exploitation） 之苦。如果我们仅仅采取贪心策略（Greedy），智能体可能会陷入局部最优的陷阱，永远无法触及未曾探索的高奖励区域。

为了解决这一矛盾，本章将利用前述的不等式，构建一套具有数理保障的探索机制。我们将以多臂老虎机（Multi-Armed Bandit, MAB）这一最简决策模型为切入点，演示霍夫丁不等式是如何演化为 UCB (Upper Confidence Bound) 算法的。

Optimism in the Face of Uncertainty

在数理决策中，OFU 原则是一套极具“进取心”的逻辑。它的核心思想是：对于任何一个动作，其真实的期望价值 $\mu_a$ 可能高于我们的经验估计 $\hat{\mu}_a$。我们不仅要看当前的平均得分，还要给那些“样本较少、不确定性较高”的动作一个额外的置信补偿。我们希望找到一个上界 $U_t(a)$，使得真实价值 $\mu_a$ 以极大的概率满足：

$$\begin{equation} \mu_a \le \hat{\mu}_a(t) + U_t(a) \end{equation}$$

算法的行为准则便是：永远选择那个“置信上限”最高的动作。从霍夫丁不等式推导 UCB 指数假设对于某个动作 $a$，我们在时间 $t$ 之前已经观察了 $N_t(a)$ 次采样。根据第三章推导出的霍夫丁不等式：

$$\mathbb{P}\left( \mu_a \ge \hat{\mu}_a(t) + \epsilon_t \right) \le \exp\left( -2 N_t(a) \epsilon_t^2 \right)$$

我们令 $\delta_t$ 代表我们允许“出错”的概率，即真实均值逃逸出我们设定的上限的概率。令：

$$\begin{equation} \exp\left( -2 N_t(a) \epsilon_t^2 \right) = \delta_t \end{equation}$$

通过对数变换求解误差项 $\epsilon_t$：

$$\begin{equation} -2 N_t(a) \epsilon_t^2 = \ln(\delta_t) \implies \epsilon_t = \sqrt{\frac{-\ln(\delta_t)}{2 N_t(a)}} \end{equation}$$

随时间衰减的出错概率在动态的决策序列中，随着总步数 $t$ 的增加，我们希望估计的准确性越来越高，即出错概率 $\delta_t$ 应该随时间衰减。在标准的 UCB1 算法中，数学家设定 $\delta_t = t^{-4}$（或者类似的幂律衰减），以确保累积遗憾（Regret）的对数收敛性。代入 $\delta_t = t^{-4}$：

$$\begin{equation} \epsilon_t = \sqrt{\frac{-\ln(t^{-4})}{2 N_t(a)}} = \sqrt{\frac{4 \ln t}{2 N_t(a)}} = \sqrt{\frac{2 \ln t}{N_t(a)}} \end{equation}$$

由此，我们推导出著名的 UCB 索引公式：

$$\begin{equation} A_t = \arg\max_{a \in \mathcal{A}} \left[ \hat{Q}_t(a) + c \sqrt{\frac{\ln t}{N_t(a)}} \right] \end{equation}$$

Temporal difference learning and the bootstrapping principle

在完成了针对经验均值缩放的定量分析后，我们已经能够利用霍夫丁不等式为“样本均值”划定置信边界。然而，蒙特卡罗（MC）方法在数理结构上存在一个内禀的缺陷：它依赖于完整轨迹的回报 $G_t$。在长序列决策任务中，$G_t$ 作为一个由大量随机奖励 $R_{t+k}$ 加权求和而成的随机变量，其累积方差会随着时间步的增加而线性增长，导致收敛效率极低。

为了克服这一“路径方差陷阱”，我们必须回到贝尔曼方程的递归本质。如果说 MC 是在路径空间进行全局积分，那么时序差分（Temporal Difference, TD）学习则是利用微分思想，将全局的价值估计坍缩为局部的时间步迭代。这一跃迁标志着强化学习从“离线轨迹平均”向“在线自举更新”的数理范式转移。

TD 学习的逻辑核心在于自举（Bootstrapping），即利用后续状态的估计值来更新当前状态的估计。这一思想直接源于第一节推导出的贝尔曼期望方程：

$$V^\pi(s) = \mathbb{E}_\pi [R_{t+1} + \gamma V^\pi(S_{t+1}) \mid S_t = s]$$

在无模型设定下，我们无法直接计算期望 $\mathbb{E}$，但可以通过环境的一次真实跃迁 $(S_t, A_t, R_{t+1}, S_{t+1})$ 获得一个即时观测。此时，我们构建一个TD 目标（TD Target） $G_t^{TD} = R_{t+1} + \gamma V(S_{t+1})$。注意，此处的 $V(S_{t+1})$ 是智能体当前的经验估计值，而非真值。

我们定义 TD 误差（TD Error） $\delta_t$ 为当前估计与单步推演后的目标之间的残差：

$$\begin{equation} \delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \end{equation}$$

基于随机逼近理论（Stochastic Approximation），我们构建如下更新规则：

$$\begin{equation} V(S_t) \leftarrow V(S_t) + \alpha \delta_t \end{equation}$$

其中 $\alpha$ 为学习率。这一公式在数学上可以被解读为对贝尔曼残差的梯度下降过程。与 MC 不同，TD 学习不需要等待回合结束，而是利用了马尔可夫性的递归特征，实现了价值信息在时域上的实时传递。

TD 学习引入自举机制后，深刻地改变了估计量的数理性质。这构成了强化学习中著名的偏置-方差权衡（Bias-Variance Tradeoff）。在蒙特卡罗方法中，目标值 $G_t = \sum \gamma^k R_{t+k+1}$ 是对真实价值 $V^\pi(s)$ 的无偏估计（Unbiased）。然而，由于 $G_t$ 受到整条路径上所有随机状态转移和奖励波动的累积影响，其方差 $\text{Var}(G_t)$ 极大，导致在有限样本下收敛速度极其缓慢。

相比之下，TD 目标 $R_{t+1} + \gamma V(S_{t+1})$ 表现出截然不同的特征：

• 低方差（Low Variance）：TD 目标仅受单步随机性（$R_{t+1}$ 和 $S_{t+1}$）的影响。后续的价值波动被当前的估计值 $V(S_{t+1})$ “抹平”了。由于只考虑一步之内的随机扰动，其方差远小于 MC 的长程累积。

• 有偏性（Biased）：在学习初期，由于 $V(S_{t+1})$ 往往是随机初始化的，TD 目标并不是对真实期望的准确估计。只有当价值函数逐渐收敛时，这种偏置才会消失。

从数理放缩的角度看，TD 学习通过引入可控的“计算性偏置”换取了“统计性方差”的剧烈下降。这解释了为什么在实际工程中，TD 方法通常比 MC 表现出更优越的样本效率，因为它在每一时刻都在利用已有的知识（自举）来缩窄未知的搜索边界。批量更新与收敛动力学在分析 TD 学习的收敛性时，一个重要的数理视角是将其视为一种算子逼近。在给定一系列采样轨迹的背景下，TD(0) 实际上是在寻找一个最优的线性函数映射，使得在这些采样样本上的贝尔曼剩余平方和最小。

对于有限状态 MDP，TD(0) 已被证明能以概率 1 收敛至真实价值 $V^\pi$。其收敛动力学遵循微分方程法（ODE Method）的描述，即 $V$ 的演化轨迹在宏观上逼近贝尔曼算子的收缩路径。与 MC 相比，TD 学习更倾向于最大似然估计（Maximum Likelihood Estimate），即它倾向于构建一个与采样数据最为契合的马尔可夫模型，并解出该模型下的精确不动点。

从单步到长程的谱系TD(0) 仅仅是价值估计谱系的一个极端（只看一步），而 MC 是另一个极端（看无穷步）。两者之间存在着广阔的中间地带——n 步时序差分（n-step TD）。

$$\begin{equation} G_{t:t+n} = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n}) \end{equation}$$

随着 $n$ 的增加，我们减少了自举带来的偏置，但增加了采样的方差。这种谱系的连续性最终催生了 TD($\lambda$) 算法，通过指数加权的方式将所有步长的 TD 目标融合在一起。至此，我们已经掌握了在采样空间与递归空间之间进行权衡的数理准则。强化学习最核心的估计工具箱——从单步自举到长程采样——已完整地呈现在我们面前。