一个笨人能理解的东西，其他人也能理解。 —— Richard Phillips Feynman

为了研究一个物体或者说系统的性质，首先必须明确它所处的状态。一般的热统书里，热力学部分常讨论的是平衡态，指的是在没有外界影响的条件下，物体的各部分的宏观性质（温度T、体积V等等）在长时间内不发生任何变化。 因为此 blog 是从第一性原理开始做推导，所以笔者这里只考虑从微观粒子（原子和分子）的运动规律，不涉及任何宏观热力学定律（如温度和熵之类的概念）。

微观世界的力学原理

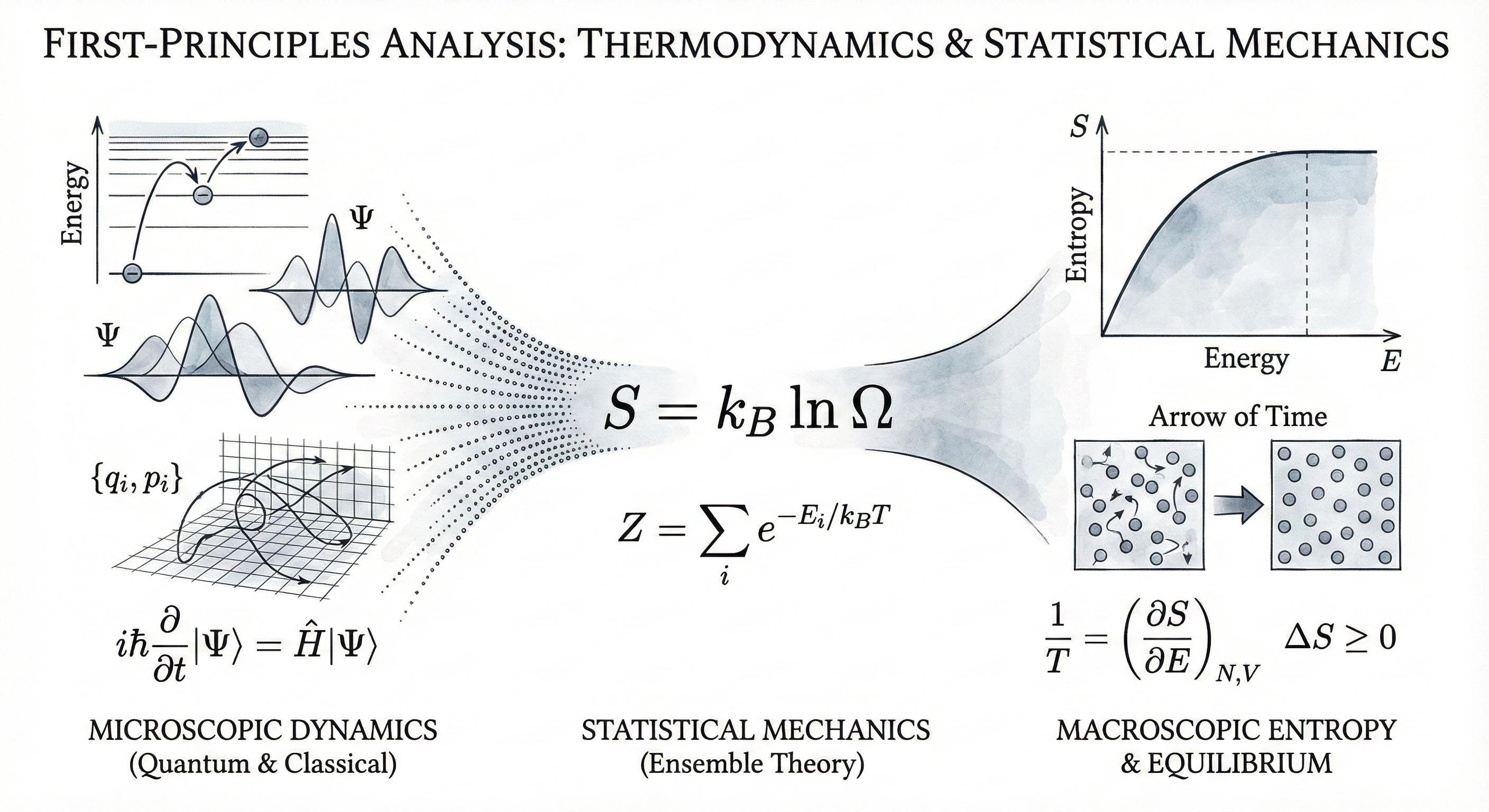
笔者这里定义一个由 $N$ 个无内部结构的粒子组成的、与外界完全隔离的系统，其被限制在体积为 $V$ 的空间内的一个环境。现在我们的首要任务是精确定义该系统在任意时刻的微观状态，并阐述其动力学演化所遵循的基本定律。这一描述构成了统计力学得以建立的力学基础，我们将分别在经典和量子两种范式下进行阐述。

在经典力学的框架内，一个由 $N$ 个粒子组成的系统的微观状态，在任意时刻 $t$ 由该时刻所有粒子的广义坐标 $\{q_i(t)\}_{i=1}^{3N}$ 和广义动量 $\{p_i(t)\}_{i=1}^{3N}$ 的集合所完全确定。为了在数学上统一处理这 $6N$ 个自由度，我们引入一个 $6N$ 维的相空间 ($\Gamma-{space}$)，其坐标轴由 $\{q_i, p_i\}$ 张成。于是，系统的一个特定微观状态便与相空间中的一个几何点一一对应。系统的动力学演化则表现为该点在相空间中的一条连续轨迹。这条轨迹的运动规律由系统的哈密顿量 $H(\{q_i\}, \{p_i\})$ 决定，该函数是系统总能量的表达。具体的运动方程即为哈密顿正则方程：

$$\begin{equation} \dot{q}_i = \frac{\partial H}{\partial p_i}, \quad \dot{p}_i = - \frac{\partial H}{\partial q_i} \quad (i = 1, \dots, 3N) \end{equation}$$

对于我们所关注的孤立系统，其总能量是守恒的，这意味着哈密顿量是一个运动常数，$H(\{q_i\}, \{p_i\}) = E$。这个能量守恒的约束条件表明，系统在相空间中的轨迹并不能遍及整个空间，而是被严格限制在由能量值 $E$ 所定义的 $6N-1$ 维等能超曲面之上。

因此，经典力学为我们提供了一套完全确定性的描述：一旦初始微观状态（即相空间中的一个初始点）被给定，系统的整个未来和过去的轨迹便被哈密顿方程唯一确定。

然而，对于构成宏观物质的原子和分子，其行为的更基本描述是由量子力学给出的。在量子力学的表述中，一个 $N$ 粒子系统的微观状态由一个定义在多粒子希尔伯特空间 $\mathcal{H}$ 中的态矢量 $|\Psi(t)\rangle$ 所完整描述。此态矢量的演化遵循薛定谔方程：

$$\begin{equation} i\hbar \frac{d}{dt}|\Psi(t)\rangle = \hat{H}|\Psi(t)\rangle \end{equation}$$

其中 $\hat{H}$ 是系统的哈密顿算符，它对应于系统的总能量可观测量。对于一个不含时的哈密顿算符（即孤立系统），该方程的定态解，或称能量本征态，满足定态薛定谔方程 $\hat{H}|\psi_n\rangle = E_n|\psi_n\rangle$。这些本征态 $|\psi_n\rangle$ 构成了一组完备的基矢，而 $E_n$ 则是系统可能具有的能量本征值，其谱可能是分立的。在此背景下，一个量子微观状态可以被定义为系统所处的某一个特定的能量本征态 $|\psi_n\rangle$。

所以，无论是经典力学还是量子力学，都为我们提供了关于孤立系统微观状态及其动力学演化的完备且确定性的理论框架。然而，正是这种理论上的完备性揭示了一个根本性的困境。对于一个宏观系统，$N$ 的数值可达阿伏伽德罗常数的量级（$\sim 10^{23}$），因此精确地确定一个系统的初始微观状态——无论是 $6N$ 个经典坐标和动量，还是一个复杂的多体波函数——在实践上是完全不可能完成的任务。更为关键的是，系统的宏观物理性质，例如压强或磁化强度，并不依赖于系统所处的某个特定的微观状态的瞬时细节。这些宏观量是大量粒子集体行为的体现，在系统处于无数个不同的微观状态时，它们可以呈现出相同或极其相近的数值。这种从一个确定的、但无法获知且信息过载的微观状态，到我们实际关心的、稳定的宏观性质之间的巨大鸿沟，表明纯粹的力学路径已无法前进。因此，理论的发展必须寻求一种范式上的转变：即从追踪单个微观态的确定性演化，转向研究在给定宏观约束下，所有可能微观状态的统计分布规律。这一转变，构成了我们下一步引入统计假设的逻辑必然性。

力学到统计的基本统计假设

尽管力学为我们提供了描述系统微观状态及其演化的完备理论，但由于初始条件的不可知性以及微观细节对于宏观性质的无关性，追踪系统在相空间中的确切轨迹，既无可能也无必要。这一结论迫使我们必须进行一次根本性的视角转换，即从关注系统所处的“那一个”具体微观状态，转向考察在给定的宏观条件下，系统“所有可能”的微观状态的集合。这个由满足特定宏观约束条件的、所有可能微观状态构成的假想集合，在物理学中被称为系综。对于我们正在研究的能量为 $E$、体积为 $V$、粒子数为 $N$ 的孤立系统，其对应的系综包含了相空间等能面上所有可能的微观态，这个特定的系综被称为微正则系综。

既然我们承认无法知晓系统究竟处于哪一个微观状态，那么唯一有意义的问题便是：在平衡态下，系统处于其中任何一个允许的微观状态的概率是多少？为了回答这个问题，我们必须引入一个超越纯粹力学范畴的假设，笔者假设是连接微观力学世界和宏观统计世界的唯一桥梁，它构成了整个统计力学的基石。这便是等概率原理，或称统计力学的基本假设。该假设的内容是：

对于一个处于热力学平衡态的孤立系统，其所有可及的微观状态出现的概率是完全相等的。

这个原理并非从力学定律逻辑推导而来，而是一个建立在更深层次的对称性和信息论基础上的公设。它的合理性根植于“无知即平等”的原则（或称“最大熵原理”）：既然哈密顿动力学演化本身（由刘维尔定理保证相空间体积元不变）并未表现出对任何特定微观状态的偏好，而且我们对系统的初始条件一无所知，那么最无偏见的、唯一合理的假设就是认为所有能量相同的微观状态都是平等的。任何非均匀的概率分布都将意味着我们掌握了某些我们实际上并不拥有的、关于系统状态的额外信息。因此，这个公设的最终正确性与合法性，需要由其导出的一整套理论体系与实验结果的精确符合来最终验证，而物理学的历史已经雄辩地证明了这一点。

基于等概率原理，我们可以立即写出系统处于任一特定微观状态 $i$ 的概率 $P_i$ 的数学表达式。若我们将一个宏观态 $(E, V, N)$ 所对应的微观状态总数记为 $\Omega(E, V, N)$，那么根据假设，对于任何一个属于该宏观态的微观状态 $i$，其出现的概率为：

$$\begin{equation} P_i = \frac{1}{\Omega(E, V, N)} \end{equation}$$

而对于能量不为 $E$ 的任何微观状态，其出现的概率则为零。这里的核心物理量 $\Omega(E, V, N)$，即等能面上的相空间体积（在量子情形下为能量为 $E$ 的量子态的简并度），成为了描述宏观态性质的关键。它量化了一个宏观状态可以由多少种微观方式来实现。

至此，我们已经完成了理论构建中至关重要的一跃。通过引入等概率假设，我们成功地将一个无法解决的动力学问题，转化为了一个在原则上可以解决的计数问题。我们不再需要去解 $10^{23}$ 个粒子耦合的运动方程，而是转而去计算与宏观态 $(E, V, N)$ 相容的微观状态总数 $\Omega$。这一步的完成，意味着我们已经为搭建完整的理论大厦奠定了统计层面的基础。现在，我们手中握有一个纯粹的统计量 $\Omega$，它完全由微观力学（通过哈密顿量）和系统的宏观参数所决定。下一步的逻辑任务，便是将这个核心的统计量 $\Omega$ 与一个可测量的宏观物理量直接联系起来，从而真正实现微观与宏观的贯通。这个联系的建立，将通过熵的定义来完成。

熵的统计定义与第二定律

在前两个part中，我们完成了从确定性力学到统计描述的过渡，其核心成果是将对孤立系统在平衡态下的描述，归结为对一个核心统计量——相容微观态总数 $\Omega(N, V, E)$ 的计算。现在，我们将这个源于微观计数的数字，与一个具有实际物理意义的、可测量的宏观状态函数联系起来。

我们寻求建立一个函数 $S(N, V, E)$，它完全由 $\Omega$ 决定，并具有宏观物理量，特别是广延量的基本属性。广延性要求，对于两个相互独立的子系统组成的复合系统，该物理量的总值应等于各子系统值之和。

让我们设想两个处于各自平衡态的、相互独立的孤立系统，分别记为系统1和系统2。它们的宏观状态由 $(N_1, V_1, E_1)$ 和 $(N_2, V_2, E_2)$ 给出，相对应的微观态数目分别为 $\Omega_1(N_1, V_1, E_1)$ 和 $\Omega_2(N_2, V_2, E_2)$。现在，若将这两个系统视为一个大的复合系统，由于两者相互独立，复合系统的任何一个微观状态都可以被看作是系统1的一个微观状态与系统2的一个微观状态的组合。因此，该复合系统的总微观态数目 $\Omega_{total}$ 等于两者之积：

$$\begin{equation} \Omega_{total}(N_1+N_2, V_1+V_2, E_1+E_2) = \Omega_1(N_1, V_1, E_1) \times \Omega_2(N_2, V_2, E_2) \end{equation}$$

我们所要寻找的宏观函数 $S$ 必须满足广延性，即 $S_{total} = S_1 + S_2$。于是，我们需要找到一个函数关系 $S=f(\Omega)$，它能够将微观态数目的乘法法则，转化为宏观物理量的加法法则。满足 $f(\Omega_1 \times \Omega_2) = f(\Omega_1) + f(\Omega_2)$ 这一函数方程的数学形式正是对数函数。因此，这个新的宏观物理量 $S$ 必须与 $\Omega$ 的对数成正比。基于此，我们给出熵 (Entropy) 的统计力学定义，即玻尔兹曼公式：

$$\begin{equation} S \equiv k_B \ln \Omega(N, V, E) \end{equation}$$

此定义中的常数 $k_B$ 被称为玻尔兹曼常数，它是一个具有能量/温度量纲的普适常数。其数值的选择是为了确保由此定义出的统计熵，与历史上由宏观热力学（通过卡诺循环和可逆过程）定义的熵在量纲和数值上完全一致。通过这个定义，熵获得了清晰而深刻的物理内涵：

一个宏观态的熵，是该宏观态所对应的微观实现方式数目的对数量度。

熵从此不再是一个仅与热量和温度相关的抽象参数，它直接量化了我们对于系统所处具体微观状态的不确定性程度。一个熵值更高的宏观态，其内部的“可能性”或“无序度”也更高。

这一定义的直接且最重要的推论，便是热力学第二定律。考虑一个孤立系统，其内部存在某种约束（例如，一个箱体被隔板分为两半，而所有气体分子初始时均位于左半侧）。系统处于此约束下的初始平衡态，对应的微观态总数为 $\Omega_{initial}$。现在，我们撤去这个内部约束（例如抽去隔板）。系统的相空间中，原本因约束而无法访问的区域现在变得可及，系统开始向新的平衡态自发演化。根据我们在第二步中建立的等概率原理，在最终达到的新平衡态下，系统将等概率地出现在所有可及的微观状态中。自然地，系统演化的方向必然是朝向包含最多微观状态数的那个宏观态，因为这个宏观态是所有可能宏观态中占据了压倒性优势的、最概然的状态（例如，气体均匀分布于整个箱体）。这意味着，对于任何在孤立系统中发生的自发过程，系统末态的微观态数 $\Omega_{final}$ 必然不会少于初态的微观态数 $\Omega_{initial}$，即 $\Omega_{final} \ge \Omega_{initial}$。将此不等式代入熵的定义式，我们便直接得到了热力学第二定律的数学表述：

$$\begin{equation} \Delta S = S_{final} - S_{initial} = k_B (\ln \Omega_{final} - \ln \Omega_{initial}) \ge 0 \end{equation}$$

至此，热力学中最核心也最神秘的定律之一——熵增原理，被清晰地揭示为其统计本质：

孤立系统的自发演化，无非是系统从一个概率较低（微观态数较少）的宏观态，向一个概率极高（微观态数极多）的宏观态的演进过程。

这种演化的不可逆性，也源于统计上的压倒性概率，而非源于任何微观力学定律的内禀不对称性。我们已经成功地从第一性原理出发，定义了熵，并推导出了第二定律，为宏观世界的“时间之箭”找到了其微观统计的起源。

热力学平衡与温度的统计诠释

现在，我们转向对温度这一概念的微观诠释。在宏观热力学中，温度是表征系统“冷热程度”的物理量，其根本作用在于判断系统间热传递的方向和是否达到热平衡。因此，一个成功的统计理论，必须能够在不预设温度概念的前提下，仅从微观态的统计分布中推导出热平衡的条件，并由此自然地引出温度的定义。

为此，我们考虑一个由两个子系统（记为系统1和系统2）构成的、与外界完全隔离的复合系统。这两个子系统之间存在一堵允许能量交换但隔绝粒子和体积变化的接触壁（即透热壁）。整个复合系统的总能量 $E_{total}$ 是恒定的。设在某一时刻，系统1的能量为 $E_1$，则系统2的能量必须为 $E_2 = E_{total} - E_1$。尽管 $E_1$ 和 $E_2$ 可以随能量交换而变化，但它们的总和始终守恒。根据我们在第三步的推导，对于一个给定的能量分配 $(E_1, E_2)$，复合系统的总熵 $S_{total}$ 是两个子系统熵的和，即：

$$\begin{equation} S_{total}(E_1) = S_1(E_1) + S_2(E_{total} - E_1) \end{equation}$$

此处的 $S_1$ 和 $S_2$ 分别是子系统1和2的统计熵。当撤除内部约束（即允许能量交换）后，根据热力学第二定律，这个孤立的复合系统将自发地向总熵最大的宏观态演化。当系统达到最终的热平衡态时，其总熵 $S_{total}$ 必然处于极大值。这意味着，任何微小的能量交换都不会再引起总熵的增加。因此，热平衡的数学条件是总熵 $S_{total}$ 对能量变量 $E_1$ 的一阶导数为零：

$$\begin{equation} \frac{\partial S_{total}}{\partial E_1} \bigg|_{\text{平衡}} = \frac{\partial S_1(E_1)}{\partial E_1} + \frac{\partial S_2(E_{total}-E_1)}{\partial E_1} = 0 \end{equation}$$

利用复合函数求导法则，我们处理第二项：$\frac{\partial S_2}{\partial E_1} = \frac{\partial S_2}{\partial E_2} \frac{dE_2}{dE_1}$。由于 $E_2 = E_{total} - E_1$，显然有 $\frac{dE_2}{dE_1} = -1$。将此结果代入，我们便得到了热平衡所必须满足的微观条件：

$$\begin{equation} \frac{\partial S_1(E_1)}{\partial E_1} = \frac{\partial S_2(E_2)}{\partial E_2} \end{equation}$$

这个结果具有极为深刻的物理意义。它表明，当两个能够交换能量的系统达到平衡时，它们各自的熵对能量的偏导数这个物理量必然相等。这昭示了该偏导数是一个具有普适性的强度量，它在平衡时处处相等。这一特性正是宏观温度所具备的。因此，我们便可以顺理成章地将热力学温度 $T$ 定义为这一统计量的函数。为了与传统热力学的符号习惯保持一致，我们定义：

$$\begin{equation} \frac{1}{T} \equiv \left(\frac{\partial S}{\partial E}\right)_{N,V} \end{equation}$$

借助这个纯粹由统计力学和微观态计数导出的温度定义，两个系统热平衡的条件 $T_1 = T_2$ 便成为一个自然的推论。不仅如此，这个定义还正确地预言了热传递的方向。若初始时 $T_1 > T_2$，则意味着 $(\frac{\partial S_1}{\partial E_1}) < (\frac{\partial S_2}{\partial E_2})$。为了使总熵 $S_{total} = S_1+S_2$ 增加，需要从导数较小的一方减去能量（$dE_1 < 0$），加到导数较大的一方（$dE_2 > 0$），这样才能使 $dS_{total} > 0$。这正对应于能量从系统1流向系统2，即热量从高温物体传向低温物体，与宏观经验完全吻合。

至此，热力学的第零定律（若A与C热平衡，B与C热平衡，则A与B也热平衡）也得到了解释，它现在仅仅是“等于”这个数学关系的传递性（$T_A=T_C$ 且 $T_B=T_C \implies T_A=T_B$）在物理学中的体现。而第一定律，即能量守恒定律，实际上是我们整个推导体系的出发点——无论是经典哈密顿量 $H$ 的守恒，还是量子定态薛定谔方程，其内在核心都是能量守恒。热力学第一定律的表达式 $\Delta U = Q + W$ 只是对一个非孤立系统能量变化（$U$即系统的内能 $E$）的两种宏观途径的划分：功（$W$）是通过改变系统的外部宏观参数（如体积）从而改变其能级结构所传递的能量；热（$Q$）则是在能级结构不变的情况下，通过系统间热接触使其在不同能级上的占据情况发生变化所传递的能量。

从孤立到开放的正则系综与配分函数

至此，我们的全部推导都建立在对孤立系统进行研究的微正则系综的框架之上。这一方法虽然在理论构建上是基础和必要的，但在实际应用中却面临着显著的困难。实验上要精确地维持一个宏观系统的总能量恒定是极其困难的，而且，即便能够做到，微正则系综中核心量 $\Omega(N, V, E)$ 的直接计算（即对等能面上的相空间体积进行积分或对简并能级进行计数）在数学上也往往非常复杂。一个在物理上更为常见、在数学上更为便利的情形是：研究一个与一个巨大热源（或称热库）保持热接触的系统。这个系统不再是孤立的，它可以与热库自由交换能量，因此其自身的能量不再是一个恒定值，而是在一个平均值附近涨落。在这种情况下，系统的宏观状态不再由 $(N, V, E)$ 描述，而是由更为贴近实验控制的参量 $(N, V, T)$ 来描述，其中温度 $T$ 由热库的性质所决定。描述这种系统的系综，被称为正则系综。

我们的任务是推导出，当一个小系统 S 与一个大热库 R 达到热平衡时，这个小系统 S 处于其某一个特定微观状态 $i$（对应能量为 $E_i$）的概率 $P_i$ 是多少。我们将由系统 S 和热库 R 组成的复合系统 (S+R) 视为一个总能量恒定为 $E_{total}$ 的孤立系统。因此，我们可以对这个复合系统应用微正则系综的等概率原理。根据该原理，复合系统处于其任何一个可及微观态的概率都相等。于是，系统 S 处于微观态 $i$ 的概率 $P_i$，将正比于当 S 处于该状态时，整个复合系统所能拥有的微观态总数。这个总数，实际上就是热库 R 在能量为 $E_R = E_{total} - E_i$ 时所拥有的微观态数目 $\Omega_R(E_{total} - E_i)$。因此，我们有：

$$\begin{equation} P_i \propto \Omega_R(E_{total} - E_i) \end{equation}$$

由于热库 R 远大于系统 S，所以 $E_i \ll E_{total}$。我们可以将热库的熵 $S_R = k_B \ln \Omega_R$ 在 $E_{total}$ 附近进行泰勒展开：

$$\begin{equation} S_R(E_{total} - E_i) \approx S_R(E_{total}) - \left(\frac{\partial S_R}{\partial E_R}\right)_{E_{total}} E_i + \dots \end{equation}$$

根据我们第四步中对温度的定义，偏导数项正是热库温度的倒数 $1/T$。代入后得到：

$$\begin{equation} k_B \ln \Omega_R(E_{total} - E_i) \approx S_R(E_{total}) - \frac{E_i}{T} \end{equation}$$

对上式两边取指数，即可得到 $\Omega_R$ 与 $E_i$ 的关系：$\Omega_R(E_{total} - E_i) \propto \exp(-E_i/k_B T)$。由于 $P_i$ 与 $\Omega_R$ 成正比，我们便得到了系统 S 处于能量为 $E_i$ 的微观态的概率正比于玻尔兹曼因子 $e^{-E_i/k_B T}$。

为了将此正比关系转化为等式，我们必须对概率进行归一化，即要求系统处于所有可能微观状态的概率之和为1。这引入了一个极为重要的归一化因子，即配分函数 (Partition Function)，记为 $Z$。

$$\begin{equation} Z(N, V, T) \equiv \sum_{j} e^{-E_j/k_B T} \end{equation}$$

此处的求和遍历系统 S 所有可能的微观状态 $j$。于是，系统处于特定微观状态 $i$ 的最终概率表达式为：

$$\begin{equation} P_i = \frac{e^{-E_i/k_B T}}{Z} \end{equation}$$

这个概率分布就是正则系综的分布函数。配分函数 $Z$ 不仅仅是一个归一化常数，它实际上是正则系综理论的核心，它将系统的微观能级信息 ($E_j$) 与宏观热力学性质直接联系起来。可以证明，一个系统的所有热力学信息都蕴含在其配分函数中。连接微观与宏观的桥梁是亥姆霍兹自由能 (Helmholtz Free Energy) $F$：

$$\begin{equation} Z(N, V, T) \equiv \sum_{j} e^{-E_j/k_B T} \end{equation}$$

一旦通过系统的微观能谱计算出配分函数 $Z$，就可以通过上式得到亥姆霍兹自由能 $F$。而根据宏观热力学的基本关系，一旦知道了 $F$ 对其自然变量 $(N, V, T)$ 的函数关系，所有其他的热力学量都可以通过求偏导数得到，例如熵 $S = -(\frac{\partial F}{\partial T})_{N,V}$，压强 $P = -(\frac{\partial F}{\partial V})_{N,T}$，以及内能 $U = F+TS$。

量子统计的数学形式:全同性原理与巨正则系综

我们理论体系的深化，要求将量子力学关于全同粒子的基本原理，严格地融入统计力学的数学框架中。在经典统计或对粒子做可分辨处理时，一个由 $N$ 个近独立粒子组成的系统的配分函数 $Z_N$，可以近似为单粒子配分函数 $Z_1 = \sum_i e^{-\beta \epsilon_i}$ 的 $N$ 次方，并通过引入一个修正因子 $1/N!$ 来粗略地解释粒子的不可分辨性，即 $Z_N \approx (Z_1)^N / N!$。然而，这种处理方式仅在高温低密度的经典极限下是有效的，一个从第一性原理出发的、普遍适用的理论，必须直接从量子多体波函数所固有的对称性出发，这从根本上改变了微观状态的计数方式。

直接在正则系综中处理这一对称性约束（即在固定总粒子数 $N$ 的条件下求和）在数学上是相当棘手的。为了更自然、更有效地处理这个问题，我们转向使用巨正则系综。该系综描述的是一个与恒温热库和粒子库都保持接触的开放系统，其宏观状态由温度 $T$、体积 $V$ 和化学势 $\mu$ 共同决定，系统的粒子数 $N$ 和能量 $E$ 都是可以涨落的。巨正则系综的配分函数 $\mathcal{Z}$ 定义为对所有可能的粒子数 $N$ 和所有对应的微观状态 $i$ 的求和：

$$\begin{equation} \mathcal{Z}(T, V, \mu) = \sum_{N=0}^{\infty} \sum_{i(N)} e^{-\beta(E_{i(N)} - \mu N)} \end{equation}$$

其中 $\beta = 1/k_B T$。在量子力学中，一个多粒子系统的微观状态，可以由一组占据数 $\{n_k\}$ 来指定，其中 $n_k$ 是占据在能量为 $\epsilon_k$ 的单粒子量子态上的粒子数目。系统的总粒子数 $N = \sum_k n_k$，总能量 $E = \sum_k n_k \epsilon_k$。将这两个关系代入巨配分函数的定义式中，我们可以将求和从对粒子数和系统状态的求和，转变为对所有可能的占据数分布的求和：

$$\begin{equation} \mathcal{Z} = \sum_{\{n_k\}} e^{-\beta \sum_k (n_k \epsilon_k - \mu n_k)} = \sum_{\{n_k\}} \prod_k \left[e^{-\beta(\epsilon_k - \mu)}\right]^{n_k} \end{equation}$$

由于总和是遍历所有可能的占据数组合，并且指数项可以写成连乘的形式，我们可以交换求和与求积的次序，从而得到一个极为优雅和强大的表达式：

$$\begin{equation} \mathcal{Z} = \prod_k \left( \sum_{n_k} \left[e^{-\beta(\epsilon_k - \mu)}\right]^{n_k} \right) \end{equation}$$

这个表达式的物理意义是，总的巨配分函数可以分解为对每一个单粒子量子态 $k$ 的独立因子的乘积。而全同粒子的量子对称性原理，此刻就体现在对括号内占据数 $n_k$ 的求和规则上。

对于费米子，泡利不相容原理要求每个单粒子态上最多只能容纳一个粒子，因此 $n_k$ 的取值只能是 $0$ 或 $1$。括号内的求和变为一个简单的两项之和：

$$\begin{equation} \sum_{n_k=0}^{1} \left[e^{-\beta(\epsilon_k - \mu)}\right]^{n_k} = 1 + e^{-\beta(\epsilon_k - \mu)} \end{equation}$$

对于玻色子，任何数量的粒子都可以占据同一个单粒子态，因此 $n_k$ 的取值可以是 $0, 1, 2, \dots, \infty$。括号内的求和构成了一个几何级数：

$$\begin{equation} \sum_{n_k=0}^{\infty} \left[e^{-\beta(\epsilon_k - \mu)}\right]^{n_k} = \frac{1}{1 - e^{-\beta(\epsilon_k - \mu)}} \end{equation}$$

将这些结果代回，我们便得到了适用于两类量子粒子的巨配分函数的最终形式。而更重要的物理量是处于能级 $\epsilon_k$ 上的平均粒子数，即占据数分布函数 $\langle n_k \rangle$。它可以通过对巨配分函数 $\mathcal{Z}$ 求导得到：$\langle n_k \rangle = -\frac{1}{\beta}\frac{\partial \ln \mathcal{Z}}{\partial \epsilon_k}$。

将上述两种情况下的 $\ln \mathcal{Z}$ 分别代入此式，我们便直接推导出了两种基本的量子统计分布函数：描述费米子系统的费米-狄拉克分布 (Fermi-Dirac Distribution)

$$\begin{equation} \langle n_k \rangle_{FD} = \frac{1}{e^{\beta(\epsilon_k - \mu)} + 1} \end{equation}$$

和描述玻色子系统的玻色-爱因斯坦分布 (Bose-Einstein Distribution)

$$\begin{equation} \langle n_k \rangle_{BE} = \frac{1}{e^{\beta(\epsilon_k - \mu)} - 1} \end{equation}$$

至此，我们已经从量子力学的全同性第一性原理出发，通过在巨正则系综框架下的严格数学推导，得出了决定宏观量子现象的微观粒子数分布规律。这标志着我们的理论体系已经完全具备了处理真实微观粒子系统所需的量子统计基础，为理解从金属电子气到黑体辐射等广泛的物理现象铺平了道路。