Introduction
这是笔者在大学二年级暑假时撰写的关于变分自编码器 (VAE) 的学习笔记。笔记全文采用 Typst 进行编写与排版,此 README 版本由 Typst 源码经 Google Gemini 辅助转换生成。可点击链接查看原本 pdf 格式内容。
Motivation
机器学习的一个主要分支是生成模型和判别模型。在判别建模中,目标是学习给定观察值的预测器,而在生成建模中,目标是解决学习所有变量All variables 的联合分布。
生成模型模拟数据在现实世界中的生成方式。在几乎每一门科学中,“建模”都被理解为通过假设理论和通过观察测试这些理论来揭示这个生成过程。例如,当气象学家为天气建模时,他们使用高度复杂的偏微分方程来表达天气的潜在物理特性。生物学家、化学家、经济学家等等也是如此。科学中的建模实际上几乎全是生成模型。
试图理解数据生成过程的另一个原因是,它自然地表达了世界的因果关系。因果关系的优点,就是它们比单纯的相关性更能概括新情况。
为了将生成模型转化为Discriminator,我们需要使用贝叶斯规则。即我们可以将生成模型的输出转换为分类任务中需要的条件概率,从而实现判别功能。
在判别方法中,我们直接学习一个与未来预测方向一致的映射。这与生成模型的方向相反。例如,可以认为一张图像在现实世界中是通过先识别物体,然后生成三维物体,再将其投影到像素网格上来生成的。
而判别模型则直接将这些像素值作为输入,并将其映射到标签上。虽然生成模型能够有效地从数据中学习,但它们往往比纯粹的判别模型对数据做出更强的假设,这通常会在模型出错时导致更高的渐近偏差(Asymptotic bias )。
因此,如果模型出错(事实上几乎总是有一定程度的误差),如果我们只关注于学习如何区分,并且我们有足够多的数据,那么纯粹的判别模型在判别任务中通常会导致更少的错误。然而,取决于数据量的多少,研究数据生成过程可能有助于指导判别器(如分类器)的训练。例如,在半监督学习的情况下,我们可能只有少量的标记样本,但有更多的未标记样本。在这种情况下,可以利用数据的生成模型来改进分类。
这种方法可以帮助我们构建有用的世界抽象,这些抽象可以用于多个后续的预测任务。这种追求数据中解缠、语义上有意义、统计上独立和因果关系的变化因素的过程,通常被称为无监督表示学习,而变分自编码器(VAE)已经广泛应用于此目的。
或者,可以将其视为一种隐式正则化形式:通过强制表示对数据生成过程有意义,我们将从输入到表示的映射过程约束在某种特定的模式中。通过预测世界这一辅助任务,我们可以在抽象层面上更好地理解世界,从而更好地进行后续的预测。
变分自编码器(VAE)可以看作是两个耦合但独立参数化的模型:编码器或识别模型 (Encoder or Recognition Model) ,以及解码器或生成模型 (Decoder or Generative Model) 。这两个模型相互支持。识别模型向生成模型提供其后验分布的近似值,后者需要这些近似值在“期望最大化”学习的迭代过程中更新其参数。反过来,生成模型为识别模型提供了一个框架,使其能够学习数据的有意义表示,包括可能的类别标签。根据贝叶斯规则,识别模型是生成模型的近似逆。
与普通的变分推断(VI)相比,VAE框架的一个优势在于识别模型(也称为推断模型)现在是输入变量的一个(随机)函数。这与VI不同,后者对每个数据实例都有一个独立的变分分布,这对于大数据集来说效率低下。识别模型使用一组参数来建模输入与潜变量之间的关系,因此被称为“摊销推断”。这种识别模型可以是任意复杂的,但由于其构造方式,只需一次从输入到潜变量的前馈传递即可完成,因此仍然相对快速。然而,我们付出的代价是,这种采样会在学习所需的梯度中引入采样噪声。
或许VAE框架最大的贡献是认识到我们可以使用现在被称为“重参数化技巧”的简单方法来重新组织我们的梯度计算,从而减少梯度中的方差。
Aim
provides a principled method for jointly learning deep latent-variable models and corresponding inference models using stochastic gradient descent .
该框架在生成建模、半监督学习和表示学习等方面有广泛的应用。
Probabilistic Models and Variational Inference
由于概率模型包含未知数且数据很少能完整地描述这些未知参数,我们通常需要对模型的某些方面假设一定程度的不确定性。这种不确定性的程度和性质通过(条件)概率分布来描述。在某种意义上,最完整的概率模型形式通过这些变量的联合概率分布来指定模型中所有变量之间的相关性和高阶依赖关系。
我们用 x \mathbf{x} x
假设观测变量 x \mathbf{x} x p ∗ ( x ) p^*(\mathbf{x}) p ∗ ( x ) p θ ( x ) p_\theta(\mathbf{x}) p θ ( x ) θ \theta θ
x ∼ p θ ( x ) \begin{equation}
\mathbf{x} \sim p_\theta(\mathbf{x})
\end{equation} x ∼ p θ ( x ) 学习最常见的是一个搜索参数 θ \theta θ p θ ( x ) p_\theta(\mathbf{x}) p θ ( x ) p ∗ ( x ) p^*(\mathbf{x}) p ∗ ( x ) x \mathbf{x} x
p θ ( x ) ≈ p ∗ ( x ) \begin{equation}
p_\theta(\mathbf{x}) \approx p^*(\mathbf{x})
\end{equation} p θ ( x ) ≈ p ∗ ( x ) Conditional Models
在分类或者回归问题上面,我们不关心无条件模型 p θ ( x ) p_\theta(\mathbf{x}) p θ ( x ) p θ ( y ∣ x ) p_\theta(y|x) p θ ( y ∣ x ) p ∗ ( y ∣ x ) p^*(y|x) p ∗ ( y ∣ x ) x \mathbf{x} x y y y x \mathbf{x} x p θ ( y ∣ x ) p_\theta(y|x) p θ ( y ∣ x ) x \mathbf{x} x y y y
p θ ( y ∣ x ) ≈ p ∗ ( y ∣ x ) \begin{equation}
p_\theta(y|\mathbf{x}) \approx p^*(y|\mathbf{x})
\end{equation} p θ ( y ∣ x ) ≈ p ∗ ( y ∣ x ) Directed Graphical Models and Neural Networks
我们使用有向概率图模型(Directed probability graph model),或贝叶斯网络。有向图模型是一种概率模型,其中所有的变量被拓扑组织成一个有向无环图。这些模型的变量的联合分布被分解为先验分布和条件分布的乘积:
p θ ( X 1 , . . . , X M ) = ∏ j = 1 M p θ ( X j ∣ P a ( X j ) ) \begin{equation}
p_\theta(\mathbf{X}_1, ..., \mathbf{X}_M) = \prod_{j=1}^{M} p_\theta(\mathbf{X}_j | P_a(\mathbf{X}_j))
\end{equation} p θ ( X 1 , ... , X M ) = j = 1 ∏ M p θ ( X j ∣ P a ( X j )) P a ( x j ) P_a(\mathbf{x}_j) P a ( x j ) j j j
Dataset
我们收集 N ≥ 1 N \ge 1 N ≥ 1 D \mathcal{D} D
D = { x ( 1 ) , x ( 2 ) , . . . , x ( N ) } ≡ { x ( i ) } i = 1 N ≡ x ( 1 : N ) \begin{equation}
\mathcal{D} = \{\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, ..., \mathbf{x}^{(N)}\} \equiv \{\mathbf{x}^{(i)}\}_{i=1}^N \equiv \mathbf{x}^{(1:N)}
\end{equation} D = { x ( 1 ) , x ( 2 ) , ... , x ( N ) } ≡ { x ( i ) } i = 1 N ≡ x ( 1 : N ) 数据集被认为由同一(不变)系统的独立测量值组成。在这种情况下,观测数据 D = { x ( i ) } i = 1 N \mathcal{D} = \{\mathbf{x}^{(i)}\}_{i=1}^N D = { x ( i ) } i = 1 N
log p θ ( D ) = ∑ x ∈ D log p θ ( x ) \begin{equation}
\log p_\theta(\mathcal{D}) = \sum_{x \in \mathcal{D}} \log p_\theta(x)
\end{equation} log p θ ( D ) = x ∈ D ∑ log p θ ( x ) Maximum Likelihood and Minibatch SGD
概率模型最常见的标准是最大对数似然(ML). Maximization of the log-likelihood criterion is equivalent to minimization of a Kullback Leibler divergence between the data and model distributions.
优化方式比较好用的方法是 stochastic gradient descent
考虑一个数据集 D \mathcal{D} D M \mathcal{M} M N M N_{\mathcal{M}} N M
在随机梯度下降中,这意味着(公式推导放在后面,不占用篇幅继续写结论):
E [ ∇ θ log p θ ( M ) ] = ∇ θ log p θ ( D ) \begin{equation}
\mathbb{E}[\nabla_\theta \log p_\theta(\mathcal{M})] = \nabla_\theta \log p_\theta(\mathcal{D})
\end{equation} E [ ∇ θ log p θ ( M )] = ∇ θ log p θ ( D ) M \mathcal{M} M D \mathcal{D} D log p θ ( M ) \log p_\theta(\mathcal{M}) log p θ ( M ) log p θ ( D ) \log p_\theta(\mathcal{D}) log p θ ( D )
对数似然无偏估计:
对于整个数据集 D \mathcal{D} D
log p θ ( D ) = ∑ x ∈ D log p θ ( x ) \begin{equation}
\log p_\theta(\mathcal{D}) = \sum_{x \in \mathcal{D}} \log p_\theta(x)
\end{equation} log p θ ( D ) = x ∈ D ∑ log p θ ( x ) 对于小批量数据 M \mathcal{M} M
log p θ ( M ) = ∑ x ∈ M log p θ ( x ) \begin{equation}
\log p_\theta(\mathcal{M}) = \sum_{x \in \mathcal{M}} \log p_\theta(x)
\end{equation} log p θ ( M ) = x ∈ M ∑ log p θ ( x ) 在期望上,小批量数据的对数似然可以近似整个数据集的对数似然:
1 N D log p θ ( D ) ≈ 1 N M log p θ ( M ) \begin{equation}
\frac{1}{N_\mathcal{D}} \log p_\theta(\mathcal{D}) \approx \frac{1}{N_\mathcal{M}} \log p_\theta(\mathcal{M})
\end{equation} N D 1 log p θ ( D ) ≈ N M 1 log p θ ( M ) 通过这样的迷你批次minibatches
1 N D log p θ ( D ) ≈ 1 N M log p θ ( M ) = 1 N M ∑ x ∈ M log p θ ( x ) \begin{equation}
\frac{1}{N_\mathcal{D}} \log p_\theta(\mathcal{D}) \approx \frac{1}{N_\mathcal{M}} \log p_\theta(\mathcal{M}) = \frac{1}{N_\mathcal{M}} \sum_{x \in \mathcal{M}} \log p_\theta(x)
\end{equation} N D 1 log p θ ( D ) ≈ N M 1 log p θ ( M ) = N M 1 x ∈ M ∑ log p θ ( x ) 1 N D ∇ θ log p θ ( D ) ≈ 1 N M ∇ θ log p θ ( M ) = 1 N M ∑ x ∈ M ∇ θ log p θ ( x ) \begin{equation}
\frac{1}{N_\mathcal{D}} \nabla_\theta \log p_\theta(\mathcal{D}) \approx \frac{1}{N_\mathcal{M}} \nabla_\theta \log p_\theta(\mathcal{M}) = \frac{1}{N_\mathcal{M}} \sum_{x \in \mathcal{M}} \nabla_\theta \log p_\theta(x)
\end{equation} N D 1 ∇ θ log p θ ( D ) ≈ N M 1 ∇ θ log p θ ( M ) = N M 1 x ∈ M ∑ ∇ θ log p θ ( x ) 小批量数据的梯度期望值等于整个数据集的梯度
假设数据集 D \mathcal{D} D N N N M \mathcal{M} M N M N_\mathcal{M} N M
整个数据集的对数似然梯度:
∇ θ log p θ ( D ) = ∇ θ ∑ i = 1 N log p θ ( x i ) = ∑ i = 1 N ∇ θ log p θ ( x i ) \begin{equation}
\nabla_\theta \log p_\theta(\mathcal{D}) = \nabla_\theta \sum_{i=1}^N \log p_\theta(x_i) = \sum_{i=1}^N \nabla_\theta \log p_\theta(x_i)
\end{equation} ∇ θ log p θ ( D ) = ∇ θ i = 1 ∑ N log p θ ( x i ) = i = 1 ∑ N ∇ θ log p θ ( x i ) 小批量数据的对数似然梯度:
∇ θ log p θ ( M ) = N N M ∑ j = 1 N M ∇ θ log p θ ( x j ) \begin{equation}
\nabla_\theta \log p_\theta(\mathcal{M}) = \frac{N}{N_\mathcal{M}} \sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)
\end{equation} ∇ θ log p θ ( M ) = N M N j = 1 ∑ N M ∇ θ log p θ ( x j ) 这里乘以 N N M \frac{N}{N_\mathcal{M}} N M N
假设我们抽取了 N M N_\mathcal{M} N M
E [ ∇ θ log p θ ( M ) ] = E [ N N M ∑ j = 1 N M ∇ θ log p θ ( x j ) ] \begin{equation}
\mathbb{E}[\nabla_\theta \log p_\theta(\mathcal{M})] = \mathbb{E}\left[\frac{N}{N_\mathcal{M}} \sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)\right]
\end{equation} E [ ∇ θ log p θ ( M )] = E [ N M N j = 1 ∑ N M ∇ θ log p θ ( x j ) ] 由于 M \mathcal{M} M
E [ ∑ j = 1 N M ∇ θ log p θ ( x j ) ] = N M E [ ∇ θ log p θ ( x ) ] \begin{equation}
\mathbb{E}\left[\sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)\right] = N_\mathcal{M} \mathbb{E}[\nabla_\theta \log p_\theta(x)]
\end{equation} E [ j = 1 ∑ N M ∇ θ log p θ ( x j ) ] = N M E [ ∇ θ log p θ ( x )] 其中 x x x D \mathcal{D} D
E [ ∇ θ log p θ ( M ) ] = E [ N N M ∑ j = 1 N M ∇ θ log p θ ( x j ) ] = N N M N M E [ ∇ θ log p θ ( x ) ] = N E [ ∇ θ log p θ ( x ) ]
\begin{align}
\mathbb{E}[\nabla_\theta \log p_\theta(\mathcal{M})] &= \mathbb{E}\left[\frac{N}{N_\mathcal{M}} \sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)\right] \\
&= \frac{N}{N_\mathcal{M}} N_\mathcal{M} \mathbb{E}[\nabla_\theta \log p_\theta(x)] \\
&= N \mathbb{E}[\nabla_\theta \log p_\theta(x)]
\end{align}
E [ ∇ θ log p θ ( M )] = E [ N M N j = 1 ∑ N M ∇ θ log p θ ( x j ) ] = N M N N M E [ ∇ θ log p θ ( x )] = N E [ ∇ θ log p θ ( x )] 由于数据点 x x x E [ ∇ θ log p θ ( x ) ] \mathbb{E}[\nabla_\theta \log p_\theta(x)] E [ ∇ θ log p θ ( x )]
N E [ ∇ θ log p θ ( x ) ] = ∑ i = 1 N ∇ θ log p θ ( x i ) = ∇ θ log p θ ( D ) \begin{equation}
N \mathbb{E}[\nabla_\theta \log p_\theta(x)] = \sum_{i=1}^N \nabla_\theta \log p_\theta(x_i) = \nabla_\theta \log p_\theta(\mathcal{D})
\end{equation} N E [ ∇ θ log p θ ( x )] = i = 1 ∑ N ∇ θ log p θ ( x i ) = ∇ θ log p θ ( D ) Coefficient proof
是为了补偿小批量数据与整个数据集的大小差异,使得梯度估计在期望值上保持一致。这里乘系数的原因是:
比例调整:由于小批量数据 M \mathcal{M} M D \mathcal{D} D N M N_\mathcal{M} N M N N N
无偏估计:这种调整确保了小批量数据梯度估计的期望值等于整体数据集的梯度,从而在期望上保持无偏。
定义整个数据集的对数似然梯度:
∇ θ log p θ ( D ) = ∇ θ ∑ i = 1 N log p θ ( x i ) = ∑ i = 1 N ∇ θ log p θ ( x i ) \begin{equation}
\nabla_\theta \log p_\theta(\mathcal{D}) = \nabla_\theta \sum_{i=1}^N \log p_\theta(x_i) = \sum_{i=1}^N \nabla_\theta \log p_\theta(x_i)
\end{equation} ∇ θ log p θ ( D ) = ∇ θ i = 1 ∑ N log p θ ( x i ) = i = 1 ∑ N ∇ θ log p θ ( x i ) 定义小批量数据的对数似然梯度:
∇ θ log p θ ( M ) = ∑ j = 1 N M ∇ θ log p θ ( x j ) \begin{equation}
\nabla_\theta \log p_\theta(\mathcal{M}) = \sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)
\end{equation} ∇ θ log p θ ( M ) = j = 1 ∑ N M ∇ θ log p θ ( x j ) 现在假设我们从数据集中随机抽取小批量数据 M \mathcal{M} M M \mathcal{M} M
E [ ∇ θ log p θ ( M ) ] = E [ ∑ j = 1 N M ∇ θ log p θ ( x j ) ] = N M E [ ∇ θ log p θ ( x ) ] \begin{equation}
\mathbb{E}[\nabla_\theta \log p_\theta(\mathcal{M})] = \mathbb{E}\left[\sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)\right] = N_\mathcal{M} \mathbb{E}[\nabla_\theta \log p_\theta(x)]
\end{equation} E [ ∇ θ log p θ ( M )] = E [ j = 1 ∑ N M ∇ θ log p θ ( x j ) ] = N M E [ ∇ θ log p θ ( x )] 为了使小批量数据的梯度在期望上等于整个数据集的梯度,我们需要将小批量数据的梯度进行比例调整。我们定义调整后的梯度估计为:
∇ ~ θ log p θ ( M ) = N N M ∑ j = 1 N M ∇ θ log p θ ( x j ) \begin{equation}
\tilde{\nabla}_\theta \log p_\theta(\mathcal{M}) = \frac{N}{N_\mathcal{M}} \sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)
\end{equation} ∇ ~ θ log p θ ( M ) = N M N j = 1 ∑ N M ∇ θ log p θ ( x j ) 我们现在计算这个调整后的梯度的期望值:
E [ ∇ ~ θ log p θ ( M ) ] = E [ N N M ∑ j = 1 N M ∇ θ log p θ ( x j ) ] = N N M E [ ∑ j = 1 N M ∇ θ log p θ ( x j ) ] = N N M N M E [ ∇ θ log p θ ( x ) ] = N E [ ∇ θ log p θ ( x ) ] \begin{align}
\mathbb{E}[\tilde{\nabla}_\theta \log p_\theta(\mathcal{M})] &= \mathbb{E}\left[\frac{N}{N_\mathcal{M}} \sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)\right] \\
&= \frac{N}{N_\mathcal{M}} \mathbb{E}\left[\sum_{j=1}^{N_\mathcal{M}} \nabla_\theta \log p_\theta(x_j)\right] \\
&= \frac{N}{N_\mathcal{M}} N_\mathcal{M} \mathbb{E}[\nabla_\theta \log p_\theta(x)] \\
&= N \mathbb{E}[\nabla_\theta \log p_\theta(x)]
\end{align} E [ ∇ ~ θ log p θ ( M )] = E [ N M N j = 1 ∑ N M ∇ θ log p θ ( x j ) ] = N M N E [ j = 1 ∑ N M ∇ θ log p θ ( x j ) ] = N M N N M E [ ∇ θ log p θ ( x )] = N E [ ∇ θ log p θ ( x )] 由于 x x x
N E [ ∇ θ log p θ ( x ) ] = ∑ i = 1 N ∇ θ log p θ ( x i ) = ∇ θ log p θ ( D ) \begin{equation}
N \mathbb{E}[\nabla_\theta \log p_\theta(x)] = \sum_{i=1}^N \nabla_\theta \log p_\theta(x_i) = \nabla_\theta \log p_\theta(\mathcal{D})
\end{equation} N E [ ∇ θ log p θ ( x )] = i = 1 ∑ N ∇ θ log p θ ( x i ) = ∇ θ log p θ ( D ) Learning and Inference in Deep Latent Variable Models
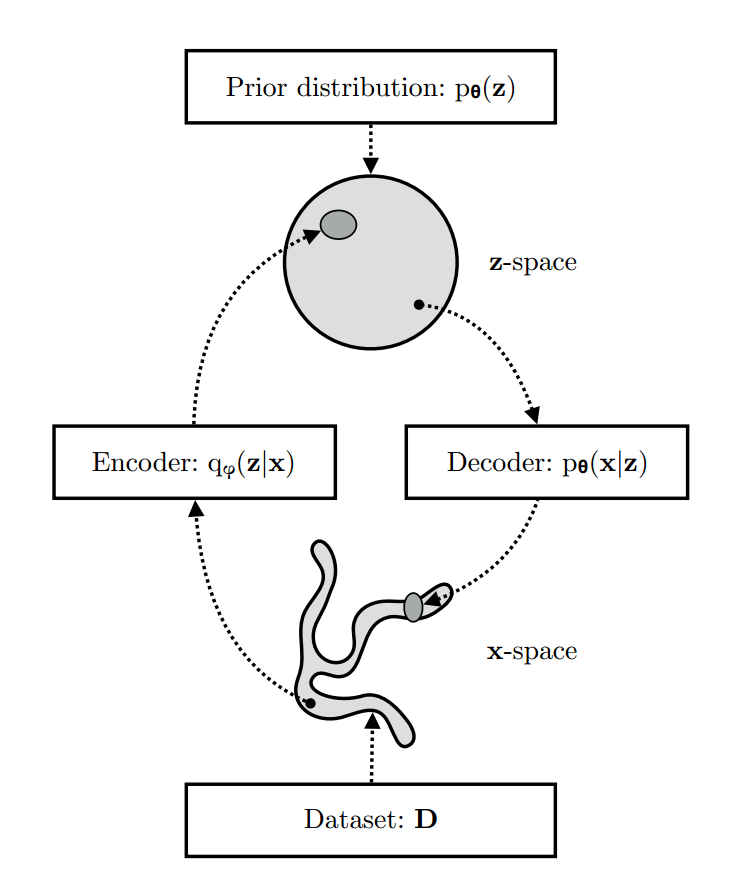
Latent Variables
我们可以将前一节讨论的完全观测有向模型扩展到包含潜变量的有向模型。潜变量是模型的一部分,但我们并不观测到它们,因此它们不属于数据集的一部分。我们通常用 z \mathbf{z} z x \mathbf{x} x x \mathbf{x} x z \mathbf{z} z p θ ( x ∣ z ) p_\theta(\mathbf{x}|\mathbf{z}) p θ ( x ∣ z ) x \mathbf{x} x
p θ = ∫ p θ ( x , z ) d z \begin{equation}
p_\theta = \int p_\theta(\mathbf{x}, \mathbf{z}) d\mathbf{z}
\end{equation} p θ = ∫ p θ ( x , z ) d z 这也被称为(单个数据点的)边缘似然或模型证据,当它作为 θ \theta θ
这种关于 x \mathbf{x} x z \mathbf{z} z p θ = ( x ∣ z ) p_\theta = (\mathbf{x}|\mathbf{z}) p θ = ( x ∣ z ) p θ ( x ) p_\theta(\mathbf{x}) p θ ( x ) z \mathbf{z} z p θ ( x ) p_\theta(\mathbf{x}) p θ ( x )
Deep Latent Variable Models
deep latent variable model (DLVM)
表示那些分布由神经网络参数化的潜变量模型 p θ ( x , z ) p_\theta(\mathbf{x}, \mathbf{z}) p θ ( x , z ) p θ ( x , z ∣ y ) p_\theta(\mathbf{x}, \mathbf{z} | \mathbf{y}) p θ ( x , z ∣ y ) p θ ( x ) p_\theta(\mathbf{x}) p θ ( x ) p ∗ ( x ) p^*(\mathbf{x}) p ∗ ( x )
或许最简单也是最常见的 DLVM 是通过以下结构指定的分解模型:
p θ ( x , z ) = p θ ( z ) p θ ( x ∣ z ) \begin{equation}
p_\theta(\mathbf{x}, \mathbf{z}) = p_\theta(\mathbf{z}) p_\theta(\mathbf{x}|\mathbf{z})
\end{equation} p θ ( x , z ) = p θ ( z ) p θ ( x ∣ z ) 其中, p θ ( z ) p_\theta(\mathbf{z}) p θ ( z ) p θ ( x ∣ z ) p_\theta(\mathbf{x}|\mathbf{z}) p θ ( x ∣ z ) p ( z ) p(\mathbf{z}) p ( z ) z \mathbf{z} z
Variational Autoencoders
Encoder or Approximate Posterior
dlvm估计这种模型中的对数似然分布和后验分布的问题。变分自编码器(VAEs)框架提供了一种计算效率高的方法来优化dlvm,并结合相应的推理模型使用SGD进行优化。
为了将DLVM的后验推理和学习问题转化为可处理的问题,我们引入了一个参数推理模型 q ϕ ( z ∣ x ) q_\phi(\mathbf{z}|\mathbf{x}) q ϕ ( z ∣ x ) ϕ \phi ϕ ϕ \phi ϕ
q ϕ ( z ∣ x ) ≈ p θ ( z ∣ x ) \begin{equation}
q_\phi(\mathbf{z}|\mathbf{x}) \approx p_\theta(\mathbf{z}|\mathbf{x})
\end{equation} q ϕ ( z ∣ x ) ≈ p θ ( z ∣ x ) 像DLVM一样,推理模型可以是(几乎)任何有向图形模型:
q ϕ ( z ∣ x ) = q ϕ ( z 1 , . . . , z M ∣ x ) = ∏ j = 1 M q ϕ ( z j ∣ P a ( z j ) , x ) \begin{equation}
q_\phi(\mathbf{z}|\mathbf{x}) = q_\phi(\mathbf{z}_1, ..., \mathbf{z}_M | \mathbf{x}) = \prod_{j=1}^{M} q_\phi(\mathbf{z}_j | P_a(\mathbf{z}_j), \mathbf{x})
\end{equation} q ϕ ( z ∣ x ) = q ϕ ( z 1 , ... , z M ∣ x ) = j = 1 ∏ M q ϕ ( z j ∣ P a ( z j ) , x ) P a ( z j ) P_a(\mathbf{z}_j) P a ( z j ) z j \mathbf{z}_j z j q ϕ ( z ∣ x ) q_\phi(\mathbf{z}|\mathbf{x}) q ϕ ( z ∣ x )
( μ , log σ ) = EncoderNeuralNet ϕ ( x ) \begin{equation}
(\mu, \log\sigma) = \text{EncoderNeuralNet}_\phi(x)
\end{equation} ( μ , log σ ) = EncoderNeuralNet ϕ ( x ) q ϕ ( z ∣ x ) = N ( z ; μ , diag ( σ ) ) \begin{equation}
q_\phi(\mathbf{z}|\mathbf{x}) = \mathcal{N}(z; \mu, \text{diag}(\sigma))
\end{equation} q ϕ ( z ∣ x ) = N ( z ; μ , diag ( σ )) 我们使用单个编码器神经网络对数据集中的所有数据点执行后验推理。这可以与更传统的变分推理方法形成对比,其中变分参数不是共享的,而是每个数据点单独迭代优化的。通过平摊推理,我们可以避免每个数据点的优化循环,并利用SGD的效率。
Evidence Lower Bound (ELBO)
VAE 通过编码器和解码器网络,利用先验分布、后验近似和重建分布,实现对复杂数据分布的近似建模和生成。
变分参数 ϕ \phi ϕ
log p θ ( x ) = E q ϕ ( z ∣ x ) [ log p θ ( x ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) p θ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) q ϕ ( z ∣ x ) q ϕ ( z ∣ x ) p θ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) q ϕ ( z ∣ x ) ] ⏟ L θ , ϕ ( x ) ("ELBO") + E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p θ ( z ∣ x ) ] ⏟ D KL ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) \begin{align}
\log p_\theta(\mathbf{x}) &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} [\log p_\theta(x)] \\
&= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[\log \frac{p_\theta(\mathbf{x},\mathbf{z})}{p_\theta(\mathbf{z}|\mathbf{x})}\right] \\
&= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[\log \frac{p_\theta(\mathbf{x},\mathbf{z})}{q_\phi(\mathbf{z}|\mathbf{x})} \frac{q_\phi(\mathbf{z}|\mathbf{x})}{p_\theta(\mathbf{z}|\mathbf{x})}\right] \\
&= \underbrace{\mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[\log \frac{p_\theta(\mathbf{x},\mathbf{z})}{q_\phi(\mathbf{z}|\mathbf{x})}\right]}_{\mathcal{L}_{\theta, \phi}(x) \text{ ("ELBO")}} + \underbrace{\mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} \left[\log \frac{q_\phi(\mathbf{z}|\mathbf{x})}{p_\theta(\mathbf{z}|\mathbf{x})}\right]}_{D_{\text{KL}}(q_\phi(\mathbf{z}|\mathbf{x}) || p_\theta(\mathbf{z}|\mathbf{x}))}
\end{align} log p θ ( x ) = E q ϕ ( z ∣ x ) [ log p θ ( x )] = E q ϕ ( z ∣ x ) [ log p θ ( z ∣ x ) p θ ( x , z ) ] = E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p θ ( x , z ) p θ ( z ∣ x ) q ϕ ( z ∣ x ) ] = L θ , ϕ ( x ) ("ELBO") E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p θ ( x , z ) ] + D KL ( q ϕ ( z ∣ x ) ∣∣ p θ ( z ∣ x )) E q ϕ ( z ∣ x ) [ log p θ ( z ∣ x ) q ϕ ( z ∣ x ) ] 第二项是 q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) p θ ( z ∣ x ) p_\theta(z|x) p θ ( z ∣ x ) q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
D KL ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) ≥ 0 \begin{equation}
D_{\text{KL}}(q_\phi(\mathbf{z}|\mathbf{x}) || p_\theta(\mathbf{z}|\mathbf{x})) \ge 0
\end{equation} D KL ( q ϕ ( z ∣ x ) ∣∣ p θ ( z ∣ x )) ≥ 0 第一项是变分下界,也称为证据下界(ELBO):
L θ , ϕ ( x ) = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) − log q ϕ ( z ∣ x ) ] \begin{equation}
\mathcal{L}_{\theta,\phi}(\mathbf{x}) = \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})} [\log p_\theta(\mathbf{x},\mathbf{z}) - \log q_\phi(\mathbf{z}|\mathbf{x})]
\end{equation} L θ , ϕ ( x ) = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) − log q ϕ ( z ∣ x )] 由于KL散度的非负性,ELBO是数据的对数似然的下界:
L θ , ϕ ( x ) = log p θ ( x ) − D KL ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) ≤ log p θ ( x ) \begin{align}
\mathcal{L}_{\theta,\phi}(\mathbf{x}) &= \log p_\theta(\mathbf{x}) - D_{\text{KL}}(q_\phi(\mathbf{z}|\mathbf{x}) || p_\theta(\mathbf{z}|\mathbf{x})) \\
&\le \log p_\theta(\mathbf{x})
\end{align} L θ , ϕ ( x ) = log p θ ( x ) − D KL ( q ϕ ( z ∣ x ) ∣∣ p θ ( z ∣ x )) ≤ log p θ ( x ) Stochastic Gradient-Based Optimization of the ELBO
ELBO的一个重要性质是,它允许使用随机梯度下降(SGD)对所有参数( ϕ \phi ϕ θ \theta θ
我们可以从 ϕ \phi ϕ θ \theta θ
L θ , ϕ ( D ) = ∑ x ∈ D L θ , ϕ ( x ) \begin{equation}
\mathcal{L}_{\theta, \phi}(\mathcal{D}) = \sum_{\mathbf{x} \in \mathcal{D}} \mathcal{L}_{\theta, \phi}(\mathbf{x})
\end{equation} L θ , ϕ ( D ) = x ∈ D ∑ L θ , ϕ ( x ) 一般来说,单个数据点ELBO及其梯度 ∇ θ , ϕ L θ , ϕ ( x ) \nabla_{\theta,\phi} \mathcal{L}_{\theta,\phi}(x) ∇ θ , ϕ L θ , ϕ ( x ) ∇ ~ θ , ϕ L θ , ϕ ( x ) \tilde{\nabla}_{\theta,\phi}\mathcal{L}_{\theta,\phi}(x) ∇ ~ θ , ϕ L θ , ϕ ( x ) θ \theta θ
∇ θ L θ , ϕ ( x ) = ∇ θ E q ϕ ( z ) [ log p θ ( z , z ) ] = E q ϕ ( z ∣ z ) [ ∇ θ ( log p θ ( x , z ) − log q ϕ ( z ∣ z ) ) ] Monte Carlo ≈ ∇ θ ( log p θ ( x , z ) − log q ϕ ( z ∣ x ) ) = ∇ θ ( log p θ ( x , z ) ) \begin{align}
\nabla_{\theta} \mathcal{L}_{\theta, \phi}(\mathbf{x}) &= \nabla_{\theta} \mathbb{E}_{q_{\phi}(\mathbf{z})} [\log p_{\theta}(\mathbf{z}, \mathbf{z})] \\
&= \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{z})} [\nabla_{\theta}(\log p_{\theta}(\mathbf{x}, \mathbf{z}) - \log q_{\phi}(\mathbf{z}|\mathbf{z}))] \\
&\text{Monte Carlo} \nonumber \\
&\approx \nabla_{\theta}(\log p_{\theta}(\mathbf{x}, \mathbf{z}) - \log q_{\phi}(\mathbf{z}|\mathbf{x})) \\
&= \nabla_{\theta}(\log p_{\theta}(\mathbf{x}, \mathbf{z}))
\end{align} ∇ θ L θ , ϕ ( x ) = ∇ θ E q ϕ ( z ) [ log p θ ( z , z )] = E q ϕ ( z ∣ z ) [ ∇ θ ( log p θ ( x , z ) − log q ϕ ( z ∣ z ))] Monte Carlo ≈ ∇ θ ( log p θ ( x , z ) − log q ϕ ( z ∣ x )) = ∇ θ ( log p θ ( x , z )) Reparameterization Trick
对于连续潜变量和可微编码器和生成模型,可以通过变量的变化直接对ELBO进行 ϕ \phi ϕ θ \theta θ
Change of variables
首先,我们将随机变量 z ∼ q ϕ ( z ∣ x ) \mathbf{z} \sim q_{\phi}(\mathbf{z}|\mathbf{x}) z ∼ q ϕ ( z ∣ x ) ϵ \epsilon ϵ z z z ϕ \phi ϕ
z = g ( ϵ , ϕ , x ) \begin{equation}
\mathbf{z} = g(\epsilon, \phi, \mathbf{x})
\end{equation} z = g ( ϵ , ϕ , x ) 其中,随机变量 ϵ \epsilon ϵ x x x ϕ \phi ϕ z z z
重新参数化技巧的主要优势在于它将不可微分的采样过程转化为可微分的参数化过程,从而使得梯度下降优化成为可能。
Algorithm 1 : ELBO的随机优化。由于噪声来源于小批量采样和 p ( ϵ ) p(\epsilon) p ( ϵ ) the Auto-Encoding Variational Bayes 算法。
Data:
D \mathcal{D} D q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) p θ ( x , z ) p_\theta(x,z) p θ ( x , z )
Result:
θ , ϕ \theta, \phi θ , ϕ
( θ , ϕ ) ← (\theta, \phi) \leftarrow ( θ , ϕ ) ←
while SGD not converged do
M ∼ D \mathcal{M} \sim \mathcal{D} M ∼ D
ϵ ∼ p ( ϵ ) \epsilon \sim p(\epsilon) ϵ ∼ p ( ϵ ) M \mathcal{M} M
Compute L ~ θ , ϕ ( M , ϵ ) \tilde{\mathcal{L}}_{\theta,\phi}(\mathcal{M},\epsilon) L ~ θ , ϕ ( M , ϵ ) ∇ θ , ϕ L ~ θ , ϕ ( M , ϵ ) \nabla_{\theta,\phi} \tilde{\mathcal{L}}_{\theta,\phi}(\mathcal{M},\epsilon) ∇ θ , ϕ L ~ θ , ϕ ( M , ϵ )
Update θ \theta θ ϕ \phi ϕ
end
Gradient of expectation under change of variable
在变量变换的基础上,我们可以将期望用新的随机变量 ϵ \epsilon ϵ
E q ϕ ( z ) [ f ( z ) ] = E p ( ϵ ) [ f ( z ) ] \begin{equation}
\mathbb{E}_{q_{\phi}(\mathbf{z})} [f(\mathbf{z})] = \mathbb{E}_{p(\epsilon)} [f(\mathbf{z})]
\end{equation} E q ϕ ( z ) [ f ( z )] = E p ( ϵ ) [ f ( z )] 其中,z = g ( ϵ , ϕ , x ) \mathbf{z}=g(\epsilon,\phi,\mathbf{x}) z = g ( ϵ , ϕ , x )
∇ ϕ E q ϕ ( z ) [ f ( z ) ] = ∇ ϕ E p ( ϵ ) [ f ( z ) ] \begin{equation}
\nabla_{\phi} \mathbb{E}_{q_{\phi}(\mathbf{z})} [f(\mathbf{z})] = \nabla_{\phi} \mathbb{E}_{p(\epsilon)} [f(\mathbf{z})]
\end{equation} ∇ ϕ E q ϕ ( z ) [ f ( z )] = ∇ ϕ E p ( ϵ ) [ f ( z )] 由于 z z z ϵ , ϕ , x \epsilon, \phi, x ϵ , ϕ , x p ( ϵ ) p(\epsilon) p ( ϵ ) ϵ \epsilon ϵ
∇ ϕ E q ϕ ( z ) [ f ( z ) ] = E p ( ϵ ) [ ∇ ϕ f ( z ) ] ≈ ∇ ϕ f ( z ) \begin{align}
\nabla_{\phi} \mathbb{E}_{q_{\phi}(\mathbf{z})} [f(\mathbf{z})] &= \mathbb{E}_{p(\epsilon)} [\nabla_{\phi} f(\mathbf{z})] \\
&\approx \nabla_{\phi} f(\mathbf{z})
\end{align} ∇ ϕ E q ϕ ( z ) [ f ( z )] = E p ( ϵ ) [ ∇ ϕ f ( z )] ≈ ∇ ϕ f ( z )
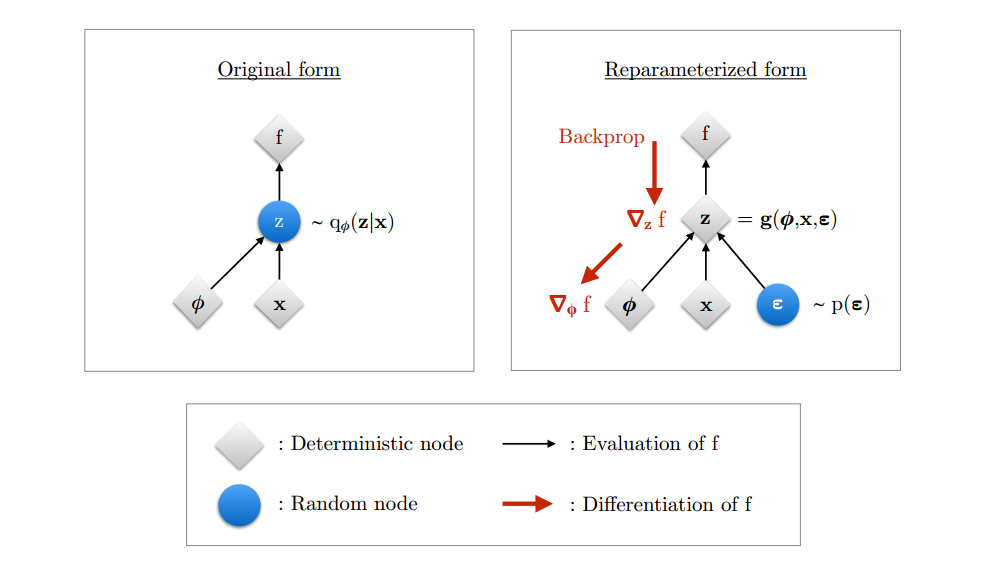
图 2 展示了重新参数化技巧的工作原理,主要包括以下两个部分:原始形式和重新参数化形式。
左图:原始形式(Original form)
节点表示:
灰色节点(Deterministic node) :表示确定性节点,如目标函数 f f f 蓝色节点(Random node) :表示随机节点,如潜变量 z z z
图示描述:
随机变量 z z z q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
目标函数 f f f z z z ϕ \phi ϕ
问题:
我们希望对目标函数 f f f ϕ \phi ϕ
由于 z z z q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) z z z ϕ \phi ϕ
右图:重新参数化形式(Reparameterized form)
节点表示:
灰色节点(Deterministic node) :表示确定性节点,如目标函数 f f f 蓝色节点(Random node) :表示随机节点,如噪声 ϵ \epsilon ϵ
图示描述:
将随机变量 z z z ϵ , ϕ , x \epsilon, \phi, x ϵ , ϕ , x z = g ( ϕ , x , ϵ ) z = g(\phi, x, \epsilon) z = g ( ϕ , x , ϵ )
ϵ \epsilon ϵ p ( ϵ ) p(\epsilon) p ( ϵ )
梯度计算:
由于 z z z ϵ , ϕ , x \epsilon, \phi, x ϵ , ϕ , x z z z
这使得我们可以对参数 ϕ \phi ϕ f f f
重新参数化技巧的步骤
变量变换:将潜变量 z z z ϵ \epsilon ϵ ϕ \phi ϕ x x x z = g ( ϵ , ϕ , x ) z = g(\epsilon, \phi,x) z = g ( ϵ , ϕ , x )
期望重写:利用变量变换,将期望用新的随机变量 ϵ \epsilon ϵ E q ϕ ( z ∣ x ) [ f ( z ) ] = E p ( ϵ ) [ f ( z ) ] \mathbb{E}_{q_\phi(z|x)} [f(z)] = \mathbb{E}_{p(\epsilon)} [f(z)] E q ϕ ( z ∣ x ) [ f ( z )] = E p ( ϵ ) [ f ( z )]
梯度计算:交换梯度运算符和期望运算符,使用蒙特卡罗采样近似期望,从而计算梯度。
重新参数化技巧的优势
使梯度计算可行:通过将采样过程外部化,使得梯度可以通过反向传播进行计算。
提高计算效率:简化梯度计算过程,使用蒙特卡罗采样进行近似估计。
Gradient of ELBO
在重新参数化的情况下,我们可以替换期望 q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) p ( ϵ ) p(\epsilon) p ( ϵ )
L θ , ϕ ( x ) = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) − log q ϕ ( z ∣ z ) ] = E p ( ϵ ) [ log p θ ( x , z ) − log q ϕ ( z ∣ x ) ] \begin{align}
\mathcal{L}_{\theta, \phi}(x) &= \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})} [\log p_{\theta}(\mathbf{x}, \mathbf{z}) - \log q_{\phi}(\mathbf{z}|\mathbf{z})] \\
&= \mathbb{E}_{p(\epsilon)} [\log p_{\theta}(\mathbf{x}, \mathbf{z}) - \log q_{\phi}(\mathbf{z}|\mathbf{x})]
\end{align} L θ , ϕ ( x ) = E q ϕ ( z ∣ x ) [ log p θ ( x , z ) − log q ϕ ( z ∣ z )] = E p ( ϵ ) [ log p θ ( x , z ) − log q ϕ ( z ∣ x )] 因此,我们可以形成单个数据点ELBO的简单蒙特卡罗估计量 L ~ θ , ϕ ( x ) \tilde{\mathcal{L}}_{\theta, \phi}(x) L ~ θ , ϕ ( x ) p ( ϵ ) p(\epsilon) p ( ϵ ) ϵ \epsilon ϵ
ϵ ∼ p ( ϵ ) z = g ( ϕ , x , ϵ ) L ~ θ , ϕ ( x ) = log p θ ( x , z ) − log q ϕ ( z ∣ x ) \begin{equation}
\epsilon \sim p(\epsilon) \\
z = g(\phi, x, \epsilon) \\
\tilde{\mathcal{L}}_{\theta, \phi}(x) = \log p_{\theta}(x, z) - \log q_{\phi}(\mathbf{z}|\mathbf{x})
\end{equation} ϵ ∼ p ( ϵ ) z = g ( ϕ , x , ϵ ) L ~ θ , ϕ ( x ) = log p θ ( x , z ) − log q ϕ ( z ∣ x ) 这一系列操作可以在TensorFlow等软件中表示为符号图,并毫不费力地微分参数 θ \theta θ ϕ \phi ϕ
该算法最初被称为**Auto-Encoding Variational Bayes (AEVB)算法。更一般地说,重新参数化的ELBO估计被称为随机梯度变分贝叶斯 *(SGVB)***估计。这个估计器也可以用来估计模型参数的后验.
Computation of log q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
ELBO(估计量)的计算需要计算密度对数 q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) x x x z z z ϵ \epsilon ϵ g ( ) g() g ( )
注意,我们通常知道密度 p ( ϵ ) p(\epsilon) p ( ϵ ) g ( . ) g(.) g ( . ) ϵ \epsilon ϵ z z z
(通过变量变换和概率密度函数的性质推导出来的,见2.4.4.1)
log q ϕ ( z ∣ x ) = log p ( ϵ ) − log d ϕ ( x , ϵ ) \begin{equation}
\log q_{\phi}(\mathbf{z}|\mathbf{x}) = \log p(\epsilon) - \log d_{\phi}(\mathbf{x}, \epsilon)
\end{equation} log q ϕ ( z ∣ x ) = log p ( ϵ ) − log d ϕ ( x , ϵ ) 其中第二项是雅可比矩阵 ∂ z ∂ ϵ \frac{\partial \mathbf{z}}{\partial \epsilon} ∂ ϵ ∂ z ϵ \epsilon ϵ z z z
log d ϕ ( x , ϵ ) = log ∣ det ( ∂ z ∂ ϵ ) ∣ \begin{equation}
\log d_{\phi}(\mathbf{x}, \epsilon) = \log \left| \det\left(\frac{\partial \mathbf{z}}{\partial \epsilon}\right) \right|
\end{equation} log d ϕ ( x , ϵ ) = log det ( ∂ ϵ ∂ z ) ∂ z ∂ ϵ = ∂ ( z 1 , . . . , z k ) ∂ ( ϵ 1 , . . . , ϵ k ) = ( ∂ z 1 ∂ ϵ 1 ⋯ ∂ z 1 ∂ ϵ k ⋮ ⋱ ⋮ ∂ z k ∂ ϵ 1 ⋯ ∂ z k ∂ ϵ k ) \begin{equation}
\frac{\partial \mathbf{z}}{\partial \epsilon} = \frac{\partial(z_1, ..., z_k)}{\partial(\epsilon_1, ..., \epsilon_k)} = \begin{pmatrix} \frac{\partial z_1}{\partial \epsilon_1} & \cdots & \frac{\partial z_1}{\partial \epsilon_k} \\ \vdots & \ddots & \vdots \\ \frac{\partial z_k}{\partial \epsilon_1} & \cdots & \frac{\partial z_k}{\partial \epsilon_k} \end{pmatrix}
\end{equation} ∂ ϵ ∂ z = ∂ ( ϵ 1 , ... , ϵ k ) ∂ ( z 1 , ... , z k ) = ∂ ϵ 1 ∂ z 1 ⋮ ∂ ϵ 1 ∂ z k ⋯ ⋱ ⋯ ∂ ϵ k ∂ z 1 ⋮ ∂ ϵ k ∂ z k deduce
假设我们有一个随机变量 z z z g g g ϵ ϵ ϵ
z = g ( ϵ , ϕ , x ) \begin{equation}
\mathbf{z} = g(\epsilon, \phi, \mathbf{x})
\end{equation} z = g ( ϵ , ϕ , x ) 根据概率密度函数的变换性质,如果 z = g ( ϵ ) z=g(\epsilon) z = g ( ϵ ) z z z q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) ϵ \epsilon ϵ p ( ϵ ) p(\epsilon) p ( ϵ )
q ϕ ( z ∣ x ) = p ( ϵ ) ∣ det ( ∂ ϵ ∂ z ) ∣ \begin{equation}
q_{\phi}(\mathbf{z}|\mathbf{x}) = p(\epsilon) \left| \det\left(\frac{\partial \epsilon}{\partial \mathbf{z}}\right) \right|
\end{equation} q ϕ ( z ∣ x ) = p ( ϵ ) det ( ∂ z ∂ ϵ ) 但是,因为我们通常是知道 ∂ z ∂ ϵ \frac{\partial z}{\partial \epsilon} ∂ ϵ ∂ z ∂ ϵ ∂ z \frac{\partial \epsilon}{\partial z} ∂ z ∂ ϵ
∣ det ( ∂ ϵ ∂ z ) ∣ = 1 ∣ det ( ∂ z ∂ ϵ ) ∣ \begin{equation}
\left| \det\left(\frac{\partial \epsilon}{\partial z}\right) \right| = \frac{1}{\left| \det\left(\frac{\partial z}{\partial \epsilon}\right) \right|}
\end{equation} det ( ∂ z ∂ ϵ ) = det ( ∂ ϵ ∂ z ) 1 密度关系表示:
q ϕ ( z ) = p ( ϵ ) ∣ det ( ∂ ϵ ∂ z ) ∣ = p ( ϵ ) 1 ∣ det ( ∂ z ∂ ϵ ) ∣ \begin{equation}
q_{\phi}(\mathbf{z}) = p(\epsilon) \left| \det\left(\frac{\partial \epsilon}{\partial z}\right) \right| = p(\epsilon) \frac{1}{\left| \det\left(\frac{\partial z}{\partial \epsilon}\right) \right|}
\end{equation} q ϕ ( z ) = p ( ϵ ) det ( ∂ z ∂ ϵ ) = p ( ϵ ) det ( ∂ ϵ ∂ z ) 1 q ϕ ( z ) = p ( ϵ ) ∣ det ( ∂ z ∂ ϵ ) ∣ − 1 \begin{equation}
q_{\phi}(\mathbf{z}) = p(\epsilon) \left| \det\left(\frac{\partial z}{\partial \epsilon}\right) \right|^{-1}
\end{equation} q ϕ ( z ) = p ( ϵ ) det ( ∂ ϵ ∂ z ) − 1 Factorized Gaussian posteriors
一个常见的选择是一个简单的factorized Gaussian encoder
q ϕ ( z ∣ x ) = N ( z ; μ , diag ( σ 2 ) ) \begin{equation}
q_{\phi}(\mathbf{z}|\mathbf{x}) = \mathcal{N}(\mathbf{z}; \mu, \text{diag}(\sigma^2))
\end{equation} q ϕ ( z ∣ x ) = N ( z ; μ , diag ( σ 2 )) 其中,μ \mu μ log σ \log\sigma log σ EncoderNeuralNet ϕ ( x ) \text{EncoderNeuralNet}_\phi(x) EncoderNeuralNet ϕ ( x )
q ϕ ( z ∣ x ) = N ( z ; μ , diag ( σ 2 ) ) \begin{equation}
q_{\phi}(\mathbf{z}|\mathbf{x}) = \mathcal{N}(\mathbf{z}; \mu, \text{diag}(\sigma^2))
\end{equation} q ϕ ( z ∣ x ) = N ( z ; μ , diag ( σ 2 )) 后验分布因子化为每个潜在变量 z i z_i z i
q ϕ ( z ∣ x ) = ∏ i q ϕ ( z i ∣ x ) = ∏ i N ( z i ; μ i , σ i 2 ) \begin{equation}
q_{\phi}(\mathbf{z}|\mathbf{x}) = \prod_i q_{\phi}(z_i|\mathbf{x}) = \prod_i \mathcal{N}(z_i; \mu_i, \sigma_i^2)
\end{equation} q ϕ ( z ∣ x ) = i ∏ q ϕ ( z i ∣ x ) = i ∏ N ( z i ; μ i , σ i 2 ) 将高斯随机变量 z z z ϵ \epsilon ϵ
ϵ ∼ N ( 0 , I ) \begin{equation}
\epsilon \sim \mathcal{N}(0, \mathbf{I})
\end{equation} ϵ ∼ N ( 0 , I ) ( μ , log σ ) = EncoderNeuralNet ϕ ( x ) \begin{equation}
(\mu, \log\sigma) = \text{EncoderNeuralNet}_{\phi}(\mathbf{x})
\end{equation} ( μ , log σ ) = EncoderNeuralNet ϕ ( x ) z = μ + σ ⊙ ϵ \begin{equation}
\mathbf{z} = \mu + \sigma \odot \epsilon
\end{equation} z = μ + σ ⊙ ϵ 从 ϵ ϵ ϵ z z z σ σ σ
∂ z ∂ ϵ = diag ( σ ) \begin{equation}
\frac{\partial z}{\partial \epsilon} = \text{diag}(\sigma)
\end{equation} ∂ ϵ ∂ z = diag ( σ ) 对角矩阵的行列式是其对角线元素的乘积,因此其对数行列式是对角线元素的对数之和:
log d ϕ ( x , ϵ ) = log ∣ det ( ∂ z ∂ ϵ ) ∣ = ∑ i log σ i \begin{equation}
\log d_{\phi}(\mathbf{x}, \epsilon) = \log \left| \det\left(\frac{\partial \mathbf{z}}{\partial \epsilon}\right) \right| = \sum_i \log \sigma_i
\end{equation} log d ϕ ( x , ϵ ) = log det ( ∂ ϵ ∂ z ) = i ∑ log σ i 后验密度为:
log q ϕ ( z ∣ x ) = log p ( ϵ ) − log d ϕ ( x , ϵ ) = ∑ i ( log N ( ϵ i ; 0 , 1 ) − log σ i ) \begin{align}
\log q_{\phi}(\mathbf{z}|\mathbf{x}) &= \log p(\epsilon) - \log d_{\phi}(\mathbf{x}, \epsilon) \\
&= \sum_i \left( \log \mathcal{N}(\epsilon_i; 0, 1) - \log \sigma_i \right)
\end{align} log q ϕ ( z ∣ x ) = log p ( ϵ ) − log d ϕ ( x , ϵ ) = i ∑ ( log N ( ϵ i ; 0 , 1 ) − log σ i ) Full-covariance Gaussian posterior
因式高斯后验可以推广为具有全协方差的高斯:
q ϕ ( z ∣ x ) = N ( z ; μ , Σ ) \begin{equation}
q_{\phi}(\mathbf{z}|\mathbf{x}) = \mathcal{N}(\mathbf{z}; \mathbf{\mu}, \mathbf{\Sigma})
\end{equation} q ϕ ( z ∣ x ) = N ( z ; μ , Σ ) 该分布的重新参数化由下式给出:
ϵ ∼ N ( 0 , I ) z = μ + L ϵ \begin{equation}
\epsilon \sim \mathcal{N}(0, \mathbf{I}) \\
\mathbf{z} = \mu + \mathbf{L}\epsilon
\end{equation} ϵ ∼ N ( 0 , I ) z = μ + L ϵ 其中 L \mathbf{L} L z z z
∂ z ∂ ϵ = L \begin{equation}
\frac{\partial z}{\partial \epsilon} = \mathbf{L}
\end{equation} ∂ ϵ ∂ z = L 因为 L \mathbf{L} L
log ∣ det ( ∂ z ∂ ϵ ) ∣ = ∑ i log ∣ L i i ∣ \begin{equation}
\log \left| \det\left(\frac{\partial \mathbf{z}}{\partial \epsilon}\right) \right| = \sum_i \log|L_{ii}|
\end{equation} log det ( ∂ ϵ ∂ z ) = i ∑ log ∣ L ii ∣ 后验密度的对数计算为:
log q ϕ ( z ∣ x ) = log p ( ϵ ) − ∑ i log ∣ L i i ∣ \begin{equation}
\log q_{\phi}(\mathbf{z}|\mathbf{x}) = \log p(\epsilon) - \sum_i \log|L_{ii}|
\end{equation} log q ϕ ( z ∣ x ) = log p ( ϵ ) − i ∑ log ∣ L ii ∣ 协方差矩阵 Σ Σ Σ
Σ = L L T \begin{equation}
\Sigma = \mathbf{L}\mathbf{L}^T
\end{equation} Σ = L L T 协方差矩阵 Σ \Sigma Σ
Σ = E [ ( z − E [ z ] ) ( z − E [ z ] ) T ] \begin{equation}
\Sigma = \mathbb{E}[(\mathbf{z} - \mathbb{E}[\mathbf{z}])(\mathbf{z} - \mathbb{E}[\mathbf{z}])^T]
\end{equation} Σ = E [( z − E [ z ]) ( z − E [ z ] ) T ] 通过引入 ϵ \epsilon ϵ
Σ = E [ ( z − E [ z ] ) ( z − E [ z ] ) T ] \begin{equation}
\Sigma = \mathbb{E}[(\mathbf{z} - \mathbb{E}[\mathbf{z}])(\mathbf{z} - \mathbb{E}[\mathbf{z}])^T]
\end{equation} Σ = E [( z − E [ z ]) ( z − E [ z ] ) T ] 由于 ϵ ∼ N ( 0 , I ) \epsilon \sim \mathcal{N}(0, \mathbf{I}) ϵ ∼ N ( 0 , I )
E [ ϵ ϵ T ] = I \begin{equation}
\mathbb{E}[\epsilon \epsilon^T] = \mathbf{I}
\end{equation} E [ ϵ ϵ T ] = I 通过神经网络获取参数 μ \mu μ log σ \log\sigma log σ L ′ \mathbf{L}' L ′
( μ , log σ , L ′ ) ← EncoderNeuralNet ϕ ( x ) \begin{equation}
(\mu, \log\sigma, \mathbf{L}') \leftarrow \text{EncoderNeuralNet}_{\phi}(\mathbf{x})
\end{equation} ( μ , log σ , L ′ ) ← EncoderNeuralNet ϕ ( x ) 构建 L \mathbf{L} L
L ← L mask ⊙ L ′ + diag ( σ ) \begin{equation}
L \leftarrow \mathbf{L}_{\text{mask}} \odot \mathbf{L}' + \text{diag}(\sigma)
\end{equation} L ← L mask ⊙ L ′ + diag ( σ ) L mask \mathbf{L}_{\text{mask}} L mask
对于因子化高斯情形,后验密度的对数计算为:
log ∣ det ( ∂ z ∂ ϵ ) ∣ = ∑ i log σ i \begin{equation}
\log \left| \det\left(\frac{\partial \mathbf{z}}{\partial \epsilon}\right) \right| = \sum_i \log \sigma_i
\end{equation} log det ( ∂ ϵ ∂ z ) = i ∑ log σ i
Algorithm 2 : 单数据点ELBO无偏估计的计算,用于具有全协方差高斯推理模型和因子化伯努利生成模型的VAE示例。L mask L_{\text{mask}} L mask
Data:
x x x ϵ \epsilon ϵ p ( ϵ ) = N ( 0 , I ) p(\epsilon) = \mathcal{N}(0,I) p ( ϵ ) = N ( 0 , I ) θ \theta θ ϕ \phi ϕ q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) p θ ( x , z ) p_\theta(x,z) p θ ( x , z )
Result:
L ~ \tilde{\mathcal{L}} L ~ L θ , ϕ ( x ) \mathcal{L}_{\theta,\phi}(x) L θ , ϕ ( x )
( μ , log σ , L ′ ) ← EncoderNeuralNet ϕ ( x ) (\mu, \log\sigma, \mathbf{L}') \leftarrow \text{EncoderNeuralNet}_\phi(x) ( μ , log σ , L ′ ) ← EncoderNeuralNet ϕ ( x )
L ← L mask ⊙ L ′ + diag ( σ ) \mathbf{L} \leftarrow \mathbf{L}_{\text{mask}} \odot \mathbf{L}' + \text{diag}(\sigma) L ← L mask ⊙ L ′ + diag ( σ )
ϵ ∼ N ( 0 , I ) \epsilon \sim \mathcal{N}(0,I) ϵ ∼ N ( 0 , I )
z ← L ϵ + μ z \leftarrow \mathbf{L}\epsilon + \mu z ← L ϵ + μ
L ~ logqz ← − ∑ i ( 1 2 ( ϵ i 2 + log ( 2 π ) + log σ i ) ) \tilde{\mathcal{L}}_{\text{logqz}} \leftarrow -\sum_i (\frac{1}{2}(\epsilon_i^2 + \log(2\pi) + \log\sigma_i)) L ~ logqz ← − ∑ i ( 2 1 ( ϵ i 2 + log ( 2 π ) + log σ i )) (Note: approximates q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
L ~ logpz ← − ∑ i ( 1 2 ( z i 2 + log ( 2 π ) ) ) \tilde{\mathcal{L}}_{\text{logpz}} \leftarrow -\sum_i (\frac{1}{2}(z_i^2 + \log(2\pi))) L ~ logpz ← − ∑ i ( 2 1 ( z i 2 + log ( 2 π ))) (Note: approximates p θ ( z ) p_\theta(z) p θ ( z )
p ← DecoderNeuralNet θ ( z ) p \leftarrow \text{DecoderNeuralNet}_\theta(z) p ← DecoderNeuralNet θ ( z )
L ~ logpx ← ∑ i ( x i log p i + ( 1 − x i ) log ( 1 − p i ) ) \tilde{\mathcal{L}}_{\text{logpx}} \leftarrow \sum_i (x_i \log p_i + (1 - x_i) \log(1 - p_i)) L ~ logpx ← ∑ i ( x i log p i + ( 1 − x i ) log ( 1 − p i )) (Note: approximates p θ ( x ∣ z ) p_\theta(x|z) p θ ( x ∣ z )
L ~ = L ~ logpx + L ~ logpz − L ~ logqz \tilde{\mathcal{L}} = \tilde{\mathcal{L}}_{\text{logpx}} + \tilde{\mathcal{L}}_{\text{logpz}} - \tilde{\mathcal{L}}_{\text{logqz}} L ~ = L ~ logpx + L ~ logpz − L ~ logqz
Estimation of the Marginal Likelihood
在训练一个VAE之后,我们可以使用抽样技术来估计模型下数据的概率。数据点的边际似然可以表示为:
log p θ ( x ) = log E q ϕ ( z ∣ x ) [ p θ ( x , z ) q ϕ ( z ∣ x ) ] \begin{equation}
\log p_{\theta}(\mathbf{x}) = \log \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})} \left[ \frac{p_{\theta}(\mathbf{x}, \mathbf{z})}{q_{\phi}(\mathbf{z}|\mathbf{x})} \right]
\end{equation} log p θ ( x ) = log E q ϕ ( z ∣ x ) [ q ϕ ( z ∣ x ) p θ ( x , z ) ] 取 q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
log p θ ( x ) ≈ log ( 1 L ∑ l = 1 L p θ ( x , z ( l ) ) q ϕ ( z ( l ) ∣ x ) ) \begin{equation}
\log p_{\theta}(\mathbf{x}) \approx \log \left( \frac{1}{L} \sum_{l=1}^{L} \frac{p_{\theta}(\mathbf{x}, \mathbf{z}^{(l)})}{q_{\phi}(\mathbf{z}^{(l)}|\mathbf{x})} \right)
\end{equation} log p θ ( x ) ≈ log ( L 1 l = 1 ∑ L q ϕ ( z ( l ) ∣ x ) p θ ( x , z ( l ) ) ) 每个 z ( l ) ∼ q ϕ ( z ∣ x ) z^{(l)} \sim q_{\phi}(z|\mathbf{x}) z ( l ) ∼ q ϕ ( z ∣ x )
每次采样都会得到一个新的隐变量 z ( l ) z^{(l)} z ( l ) l l l p θ ( x , z ( l ) ) q ϕ ( z ( l ) ∣ x ) \frac{p_{\theta}(\mathbf{x}, z^{(l)})}{q_{\phi}(z^{(l)}|\mathbf{x})} q ϕ ( z ( l ) ∣ x ) p θ ( x , z ( l ) ) L L L
Marginal Likelihood and ELBO as KL Divergences
边缘似然是一个很难直接计算的量,通过ELBO的优化,可以间接优化边缘似然。提高ELBO的紧密性,即减少ELBO和真实边缘似然之间的差距
提高ELBO潜在紧密性的一种方法是增加生成模型的灵活性。(生成模型的灵活性决定了其拟合数据分布的能力),这可以通过ELBO和KL散度之间的联系来理解。
重点会解释Evidence Lower Bound, ELBO 和Kullback-Leibler 是如何与变分自编码器(VAE)中的边缘似然(Marginal Likelihood)相关的。阐述如何通过提高生成模型的灵活性来增强ELBO的紧密性,并提供了ELBO和KL散度之间的数学联系.
边缘似然和最大似然准则:
对于一个独立同分布的(i.i.d.)数据集 D \mathcal{D} D N D N_\mathcal{D} N D
log p θ ( D ) = 1 N D ∑ x ∈ D log p θ ( x ) = E q D ( x ) [ log p θ ( x ) ] \begin{align}
\log p_{\theta}(\mathcal{D}) &= \frac{1}{N_{\mathcal{D}}} \sum_{x \in \mathcal{D}} \log p_{\theta}(x) \\
&= \mathbb{E}_{q_{\mathcal{D}}(x)}[\log p_{\theta}(x)]
\end{align} log p θ ( D ) = N D 1 x ∈ D ∑ log p θ ( x ) = E q D ( x ) [ log p θ ( x )] 这里的 q D ( x ) q_\mathcal{D}(x) q D ( x )
经验数据分布:
q D ( x ) = 1 N ∑ i = 1 N q D ( i ) ( x ) \begin{equation}
q_{\mathcal{D}}(x) = \frac{1}{N} \sum_{i=1}^{N} q_{\mathcal{D}}^{(i)}(x)
\end{equation} q D ( x ) = N 1 i = 1 ∑ N q D ( i ) ( x ) 每个组件 q D ( i ) ( x ) q_\mathcal{D}^{(i)}(x) q D ( i ) ( x ) x ( i ) x^{(i)} x ( i ) x ( i ) x^{(i)} x ( i )
数据分布和模型分布之间的KL散度可以写成:
D K L ( q D ( x ) ∣ ∣ p θ ( x ) ) = − E q D ( x ) [ log p θ ( x ) ] + E q D ( x ) [ log q D ( x ) ] = − log p θ ( D ) + 常数 \begin{align}
D_{KL}(q_{\mathcal{D}}(x) || p_{\theta}(x)) &= -\mathbb{E}_{q_{\mathcal{D}}(x)}[\log p_{\theta}(x)] + \mathbb{E}_{q_{\mathcal{D}}(x)}[\log q_{\mathcal{D}}(x)] \\
&= -\log p_{\theta}(\mathcal{D}) + \text{常数}
\end{align} D K L ( q D ( x ) ∣∣ p θ ( x )) = − E q D ( x ) [ log p θ ( x )] + E q D ( x ) [ log q D ( x )] = − log p θ ( D ) + 常数 这里的常数是 − H ( q D ( x ) ) -\mathcal{H}(q_{\mathcal{D}}(x)) − H ( q D ( x )) log p θ ( D ) \log p_\theta(\mathcal{D}) log p θ ( D )
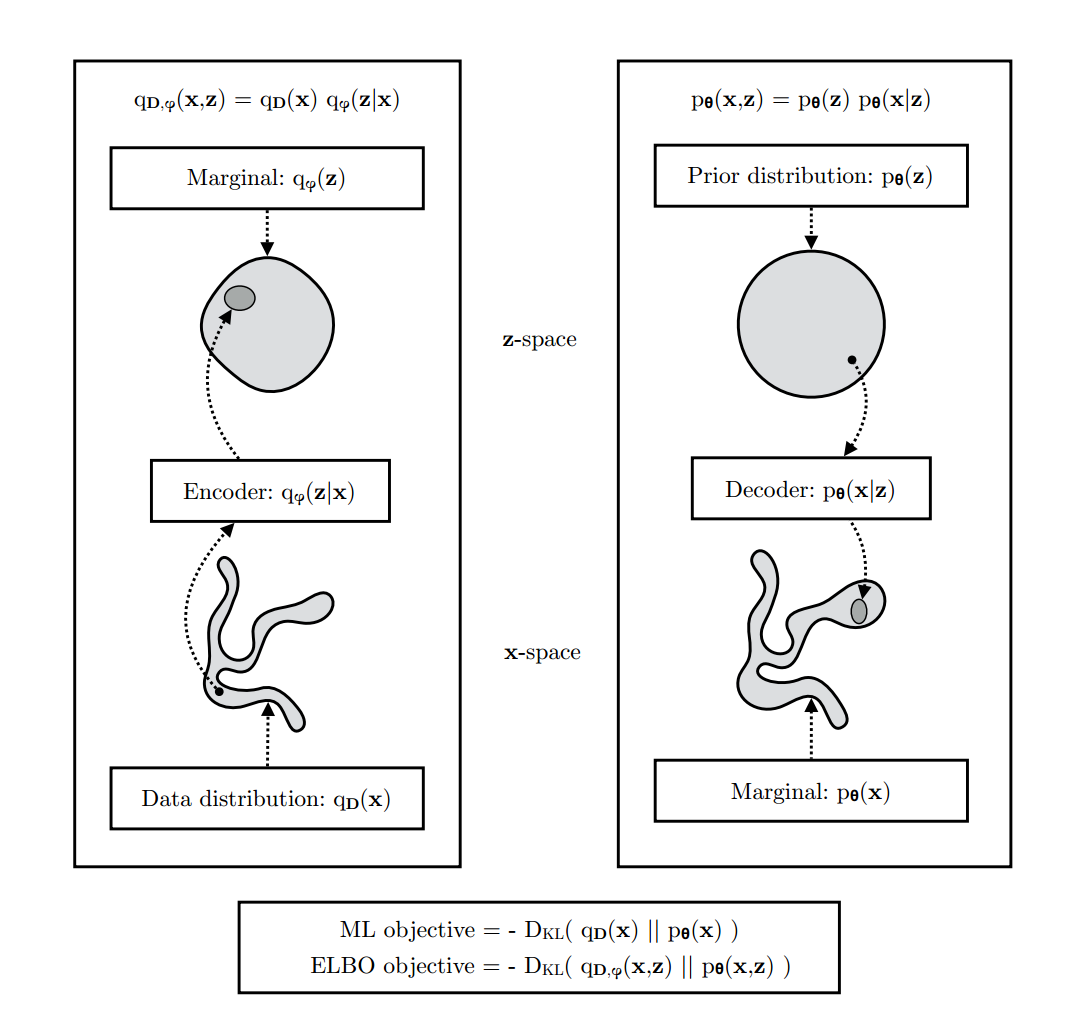
通过结合经验数据分布 q D ( x ) q_D(x) q D ( x ) q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) x x x z z z
q D , ϕ ( x , z ) = q D ( x ) q ϕ ( z ∣ x ) \begin{equation}
q_{\mathcal{D}, \phi}(x, z) = q_{\mathcal{D}}(x) q_{\phi}(z|x)
\end{equation} q D , ϕ ( x , z ) = q D ( x ) q ϕ ( z ∣ x ) 而对于 q D , ϕ ( x , z ) q_{\mathcal{D},\phi}(x,z) q D , ϕ ( x , z ) p θ ( x , z ) p_\theta(x,z) p θ ( x , z )
D K L ( q D , ϕ ( x , z ) ∥ p θ ( x , z ) ) = − E q D ( x ) [ E q ϕ ( z ∣ x ) [ log p θ ( x , z ) − log q ϕ ( z ∣ x ) ] ] − E q D ( x ) [ log q D ( x ) ] = − L θ , ϕ ( D ) + 常数 \begin{align}
& D_{KL}\!\left(q_{\mathcal{D}, \phi}(x, z) \,\|\, p_{\theta}(x, z)\right) \nonumber \\
&\qquad = - \mathbb{E}_{q_{\mathcal{D}}(x)}\!\left[ \mathbb{E}_{q_{\phi}(z|x)}\!\left[ \log p_{\theta}(x, z) - \log q_{\phi}(z|x) \right] \right] - \mathbb{E}_{q_{\mathcal{D}}(x)}\!\left[ \log q_{\mathcal{D}}(x) \right] \\
&\qquad = - \mathcal{L}_{\theta, \phi}(\mathcal{D}) + \text{常数}
\end{align}
D K L ( q D , ϕ ( x , z ) ∥ p θ ( x , z ) ) = − E q D ( x ) [ E q ϕ ( z ∣ x ) [ log p θ ( x , z ) − log q ϕ ( z ∣ x ) ] ] − E q D ( x ) [ log q D ( x ) ] = − L θ , ϕ ( D ) + 常数 常数是 − H ( q D ( x ) ) -\mathcal{H}(q_{\mathcal{D}}(x)) − H ( q D ( x ))
最大似然和ELBO目标之间的关系可以总结如下:
D K L ( q D , ϕ ( x , z ) ∣ ∣ p θ ( x , z ) ) = D K L ( q D ( x ) ) + E q D ( x ) [ D K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) ] ≥ D K L ( q D ( x ) ∣ ∣ p θ ( x ) ) \begin{align}
D_{KL}(q_{\mathcal{D}, \phi}(x, z) \,||\, p_{\theta}(x, z)) &= D_{KL}(q_{\mathcal{D}}(x)) \nonumber \\
&\quad + \mathbb{E}_{q_{\mathcal{D}}(x)}\!\left[ D_{KL}(q_{\phi}(z|x) \,||\, p_{\theta}(z|x)) \right] \\
&\ge D_{KL}(q_{\mathcal{D}}(x) \,||\, p_{\theta}(x))
\end{align} D K L ( q D , ϕ ( x , z ) ∣∣ p θ ( x , z )) = D K L ( q D ( x )) + E q D ( x ) [ D K L ( q ϕ ( z ∣ x ) ∣∣ p θ ( z ∣ x )) ] ≥ D K L ( q D ( x ) ∣∣ p θ ( x )) ELBO可以被视为在一个扩展空间中的最大似然目标。对于某个固定的编码器 q ϕ ( x ∣ z ) q_\phi(x|z) q ϕ ( x ∣ z ) p θ ( x , z ) p_\theta(x,z) p θ ( x , z ) x x x z z z
Challenges
Optimization issues
我们发现具有未修改下界目标的随机优化可能陷入不希望的稳定平衡。在训练开始时,似然项 log p ( x ∣ z ) \log p(x|z) log p ( x ∣ z ) q ( z ∣ x ) ≈ p ( z ) q(z|x) \approx p(z) q ( z ∣ x ) ≈ p ( z )
后来提出的解决方案是使用一个优化调度,其中潜在成本 D KL ( q ( z ∣ x ) ∣ ∣ p ( z ) ) D_{\text{KL}}(q(z|x) || p(z)) D KL ( q ( z ∣ x ) ∣∣ p ( z ))
潜在维度被划分为 K K K λ \lambda λ
而最大似然目标*(ML objective)*可以看作是最小化 D K L ( q D ( x ) ∣ ∣ p θ ( x ) ) D_{KL}(q_{\mathcal{D}}(x) || p_{\theta}(x)) D K L ( q D ( x ) ∣∣ p θ ( x )) q D ( x ) q_D(x) q D ( x ) p θ ( x ) p_\theta(x) p θ ( x )
ELBO目标可以看作是最小化 D K L ( q D , ϕ ( x , z ) ∣ ∣ p θ ( x , z ) ) D_{KL}(q_{\mathcal{D}, \phi}(x, z) || p_{\theta}(x, z)) D K L ( q D , ϕ ( x , z ) ∣∣ p θ ( x , z )) q D , ϕ ( x , z ) = q D ( x ) q ϕ ( z ∣ x ) q_{\mathcal{D},\phi}(x,z) = q_D(x)q_\phi(z|x) q D , ϕ ( x , z ) = q D ( x ) q ϕ ( z ∣ x )
因为KL散度的方向,完美拟合是不可能的,那么 p θ ( x , z ) p_\theta(x,z) p θ ( x , z ) q D , ϕ ( x , z ) q_{\mathcal{D},\phi}(x,z) q D , ϕ ( x , z )
左图(编码过程):
数据分布 q D ( x ) q_D(x) q D ( x )
编码器 q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x )
边缘分布 q ϕ ( z ) q_\phi(z) q ϕ ( z )
数据 x x x q D ( x ) q_D(x) q D ( x ) q ϕ ( z ∣ x ) q_\phi(z|x) q ϕ ( z ∣ x ) z z z q ϕ ( z ) q_\phi(z) q ϕ ( z )
右图:(解码过程)
先验分布 p θ ( z ) p_\theta(z) p θ ( z )
解码器 p θ ( x ∣ z ) p_\theta(x|z) p θ ( x ∣ z )
边缘分布 p θ ( x ) p_\theta(x) p θ ( x )
先验分布 p θ ( z ) p_\theta(z) p θ ( z ) z z z p θ ( x ∣ z ) p_\theta(x|z) p θ ( x ∣ z ) z z z x x x p θ ( x ) p_\theta(x) p θ ( x )
Blurriness of generative model
2.7里面提到,优化ELBO相当于最小化 D KL ( q D , ϕ ( x , z ) ∣ ∣ p θ ( x , z ) ) D_{\text{KL}}(q_{\mathcal{D},\phi}(x, z)||p_{\theta}(x, z)) D KL ( q D , ϕ ( x , z ) ∣∣ p θ ( x , z )) q D , ϕ ( x , z ) q_{\mathcal{D},\phi}(x, z) q D , ϕ ( x , z ) p θ ( x , z ) p_\theta(x, z) p θ ( x , z ) p θ ( x , z ) p_\theta(x, z) p θ ( x , z ) p θ ( x ) p_\theta(x) p θ ( x ) q D , ϕ ( x , z ) q_{\mathcal{D},\phi}(x, z) q D , ϕ ( x , z ) q D , ϕ ( x ) q_{\mathcal{D},\phi}(x) q D , ϕ ( x )
如果 ( x , z ) (x,z) ( x , z ) q D , ϕ q_{\mathcal{D},\phi} q D , ϕ p θ p_\theta p θ E q D , ϕ ( x , z ) [ log p θ ( x , z ) ] \mathbb{E}_{q_{\mathcal{D},\phi}(\mathbf{x}, \mathbf{z})} [\log p_{\theta}(\mathbf{x}, \mathbf{z})] E q D , ϕ ( x , z ) [ log p θ ( x , z )] ( x , z ) (x, z) ( x , z ) q D , ϕ q_{\mathcal{D},\phi} q D , ϕ
因此,"模糊性"问题可以通过选择一个足够灵活的推理模型和/或一个足够灵活的生成模型来解决。